定義
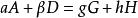速率常數假設基元反應為：
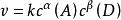速率常數
速率常數其數學表達式為:
上式中的k稱為反應速率常數又稱速率常數 k或 λ是化學反應速率的量化表示方式，其物理意義使其數值相當於參加反應的物質都處於單位濃度(1 mol·L )時的反應速率，故又稱為反應的比速率（specific reaction rate）。
不同反應有不同的速率常數，速率常數與反應溫度、反應介質（溶劑）、催化劑等有關，甚至會隨反應器的形狀、性質而異。與濃度無關，但受溫度、催化劑、固體表面性質等因素的影響。
單位
速率係數的單位取決於反應的總級數：
對零級反應，速率係數的單位是mol·L ·s 或 mol·dm ·s
對一級反應，速率係數的單位是s
對二級反應，速率係數的單位是L·mo ·s 或 dm·mol ·s
對n級反應，速率係數的單位是mol ·L ·s或 mol ·dm s
套用
速率常數k是化學動力學中一個重要的物理量，其數值直接反映了速率的快慢。質量作用定律只適用於基元反應，不適用於複雜反應。複雜反應可用實驗法決定起速率方程和速率常數。要獲得化學反應的速率方程，首先需要收集大量的實驗數據，然後在經歸納整理而得。它是確定反應機理的主要依據，在化學工程中，它又是設計合理的反應器的重要依據。
測定方法
要獲得化學反應的速率方程，首先需要通過實驗收集一套c~t或v~c數據，然後再經歸納整理計算而得反應速率常數。反應速率常數的測定方法很多，常用的有積分法和微分法。
1.積分法
利用速率方程的積分公式來確定反應級數和速率常數。是一種嘗試法。
（1）代入試差法
實驗數據代入某一級數速率方程的積分式中計算k值。
（2）作圖試差法
利用濃度函式(如一級反應中的lndCA,0CA、lnCA)對t作圖，若圖形是直線，則可由該圖形的縱軸上的截距確定反應速率常數。同時可確定反應級數。這種方法對於簡單整數級反應效果較好。但嘗試不準需再試，方法較繁。並且在數據範圍不大時，往往不同級數難以區分。這時可以用微分法。
2.微分法
對有如下通式的反應υ=-dCAdt=KCnA兩邊取對數lg-dCAdt×[t][C]××=lgk[k]+nlgCA[C]定溫下，確定反應的k和n均為常數，以lg-dCAdt×[t][C]××對lgCA[C]作圖，應為直線。斜率為反應級數n，截距lgk[k]，可求k。
