通用網論
正文
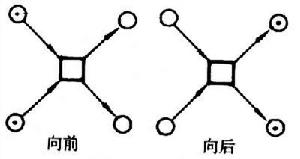
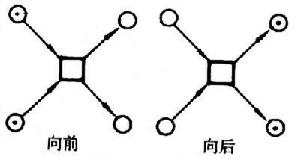
條件事件系統(簡稱CE系統)若限制佩特里網(見佩特里網論)為簡單網,且要求它的各個圓圈節點之容量均為1,就可把這些圓圈理解為條件,其中碼子的出現與否反映條件是否成立。若這種網的可到達狀態集使得任何條件均有成立與不成立的機會,任何事件也都有實施的機會,而且從任一可達狀態可以到達任何別的可到達狀態,那么這種網就是一個CE系統,一般用(B,E,F,C)表示,其中B,E分別為條件集合及事件集合;F是流關係;C是可到達狀態集。這時條件仍用圓圈圖示,事件則用方框(□)表示。一般短線代表不能分解的基本事件,方框表示有可能進一步分解的事件(或變遷)。基本情況 根據佩特里網論規定的變遷實施規則,CE系統中的事件有以下五種基本情況。
① 具備條件。
 通用網論
通用網論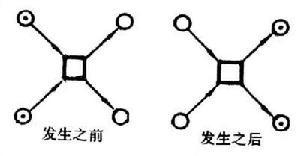 通用網論
通用網論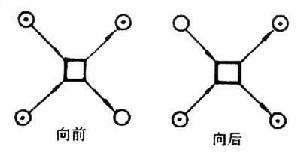 通用網論
通用網論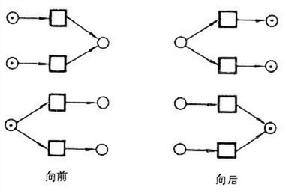 通用網論
通用網論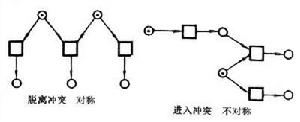 通用網論
通用網論 並發關係。
並發關係。 出現網 出現網是不帶標識的佩特里網,而且要求流關係F不含循環,要求每個圓圈至多有一個輸入地點和一個輸出地點。若令出現網節點之集合為X,那么對任何x,y∈X,若x厵y且能沿流關係F從x到y, 就說x小於y,記作x<y。由於F不含循環,所以x<y和y<x不能同時成立。
並發關係 若x,y∈X,但x
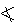 y∧y
y∧y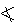 x,就說x和y並發,記作x∝y。CE系統中a,b兩件事若同時具備條件且互不衝突,它們是並發的;若a,b為可以同時含有碼子的條件,那么它們也是並發的;若a為條件而b為事件,只要a在b發生之前和之後均成立,a和b也是並發的。CE系統兩事件間的並發關係可以用它們的同步距離來定量地描述。
x,就說x和y並發,記作x∝y。CE系統中a,b兩件事若同時具備條件且互不衝突,它們是並發的;若a,b為可以同時含有碼子的條件,那么它們也是並發的;若a為條件而b為事件,只要a在b發生之前和之後均成立,a和b也是並發的。CE系統兩事件間的並發關係可以用它們的同步距離來定量地描述。 同步距離 若a,b為某CE系統中的兩組事件,a,b間的同步距離定義是該系統任何進程中 a組事件發生的次數與b組事件發生的次數之差的絕對值之最大者,若不存在最大值則為無窮。同步距離用 σ(a,b)表示,因為σ 滿足距離公理,故稱同步距離。交替發生的兩事件同步距離為1,並發事件間同步距離≥2。同步距離為1的一切事件偶(a,b)所成立集稱為CE系統的最小集合。
網拓撲和網射 將CE系統之進程記錄下來,可得到該系統的一個出現網;將出現網摺疊,可得其CE系統。摺疊是一種網射。網射是保持流關係的網連續映射。這裡連續是對網上的拓撲而言的。網拓撲滿足通常的拓撲公理,只是將“任意有限個開集的交集仍是開集”這條公理中的“有限”二字去掉。若規定CE系統中的條件為開集,凡同時包含事件及其輸入輸出條件的集合也是開集,那么CE系統的節點集合滿足網拓撲公理。網拓撲又叫佩特里拓撲,其作用是有限個點構成的空間也可以是連續的,通用網論期望藉此溝通離散模型和連續模型之間的鴻溝。通用網論已在許多學科獲得廣泛的套用。