逐次線性化

逐次線性化是指若目標函式及約束條件在某一個可行點附近線性化後得出的解點仍然保持在可行域之內，則在這一解點附近重新將目標函式及約束條件進行線性化，得出並求解新的線性規劃問題。如此繼續下去，當逐次得出的解點都保持在可行域內時，則可望這些解點能逐次逼近原非線性規劃問題的極小點的方法。

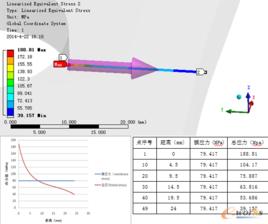
計算方法

目標函式及約束條件在某一個可行點附近線性化後得出的解點，則在這一點附近將函式或者約束條件進行線性化。

當解點超出可行域範圍時，增加一個限制步長的約束條件，計算中每次疊代所用的步長可以先取用前次疊代的數值，若解點超出可行域則減少這一數值重新求解該線性規劃問題，直到滿足收斂要求並得出極值點。

步長限值的取值對算法的成功與否有很大影響，由於一般都採用較小的步長，所以又稱小步長梯度法。實踐證明這種方法在目標函式為凸函式且可行域為凸集的情況下是收斂的，然而其確切的收斂性能尚未得到充分證明。另外這種方法所需要的疊代次數通常比較多，計算工作量也比較大，且花費的時間也比較多。

示例

逐次線性化

假設有在數值逼近學科中，拉格朗日插值能夠得到n次插值多項式，然而，每當有新的節點增加， 原來的計算出的數據均不能利用，需要重新計算，為了克服這個缺點，提出了逐次線性化插值法，由於插值多項式的存在唯一，利用逐次線性插值求出的插值多項式和拉格朗日插值多項式相同。

通過這些點做逐次線性插值，其大體思想如下：

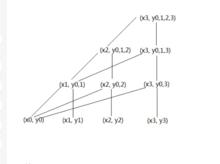圖2.逐次線性化插值思路

疊代公式：

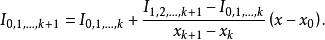逐次線性化