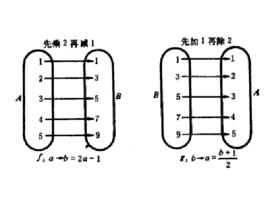
定義
 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應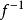 逆對應
逆對應設是集合到的一個對應,若將的方向反轉後,能得到集合到的一個對應,則稱此對應是的 逆對應,記作。
 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應 逆對應
逆對應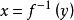 逆對應
逆對應由解析式給出的到的對應,若能由此求出用表示的新解析式,且是到的對應,則它就是的逆對應,記為。
逆對應又叫 逆映射,而映射就是單值對應,所以逆對應也是單值對應,由於從A到B的一一對應,使得B中的每一個元素在A中都有原象而且都只有唯一的原象,所以當我們把B中的“象”改為“原象”,把A中的“原象”改為它原來的象的“象”,即把對應方向反過來的時候,所得的對應仍是單值對應,這說明: 只有一一對應才有逆對應,而那些不是一 一對應的單值對應就沒有逆對應 。
相關性質及分析
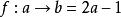 逆對應
逆對應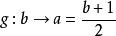 逆對應
逆對應從圖1所示的兩個對應容易看出,這兩個對應是從集合A到集合B與集合B到集合A的 單值對應。並且對應與對應的方向相反,這種方向相反的對應稱為 逆對應 。
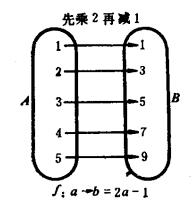 圖1(a)
圖1(a)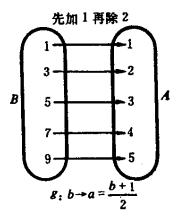 圖1(b)
圖1(b)再看圖2所示的兩個對應,圖(b)是圖(a)的逆對應,圖(a)是單值對應,而它的逆對應圖(b)不是單值對應。所以 一個單值對應,其逆對應不一定是單值對應,只有一一對應的逆對應才是單值對應 。
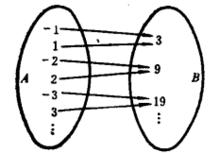 圖2(a)
圖2(a)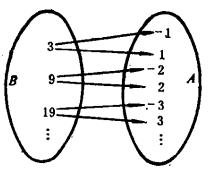 圖2(b)
圖2(b)一一對應與逆對應
多一對應 不一定有逆對應,若有,也不是單值對應。
一一對應必有逆對應,且也是一一對應,故當二集合可建立一一對應時,就說這二集合是一一對應集合。
一一對應在日常生活和生產實踐中套用很多。如某場電影的觀眾集合和電影院的座位集合是一一對應的,它通過出售電影票來建立。又如溫度計建立了溫度度數集合和水銀柱長度集合間的一一對應,從而可用水銀柱長度表示溫度。由此可知,如果由某物理量組成的集合與由某幾何量組成的集合間能建立一一對應,那么就可用該幾何量來表示物理最,這在實踐上帶來很大方便,如許多儀表(電壓計、水量計等)的設計就是如此。又如各類計算工具都是用各種不同的物理量( 如長度、轉角、電流和電壓等)去代替被計算的數值。在計算尺上代替數值的是長度;在手搖計算機上代替數值的是轉角;電子計算機套用的是電流和電壓,在那裡,使“高壓”與“1”對應,“低壓”與“0 ”對應,再利用某些特殊的裝置就能對二進制數進行運算了。一般說,如果集合A 與集合B 之間,能建立一一對應,那么集合A 的元素就可用集合B 的元素來表示,反之亦然,因此集合A 的元素與集合B 的元素可看作為同一件事。這個事實,對研究數學理論也帶來了許多方便,我們知道,在中學數學裡,由於直角坐標系的建立,下面一系列集合間能建立一一對應:
{實數} 與 {數軸上的點}
{有序實數對} 與 {坐標平面上的點}
{複數} 與 {起點在原點的平面向量}
{函式、方程} 與 {函式、方程的圖象}
等等,在這一系列集合中,前者是“數”的集合,後者是“形”的集合。人們根據需要常把研究“形”的問題轉化為研究“數”的問題,如解析幾何; 反之,研究“數”的問題也可轉化為研究“形”的問題,如方程、不等式的圖象解法等。集合之間的一一對應在許多高等數學中用處更大,在此就不再累述了。
最後應該指出,利用一一對應的觀點,使某些數學理論套用到生產實踐中去才成為可能,邏輯代數的套用就是一個實例 。
怎樣由一一對應的對應法則求它的逆對應的對應法則?
要回答這個問題是很困難的,因為各個一一對應的對應法則千差萬別,所以只能根據各個一一對應的具體情況確定求它的逆對應法則的具體方法。如果一一對應的對應法則是一個簡單的二元方程,它們的逆對應的對應法則是容易求出來的。
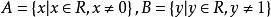 逆對應
逆對應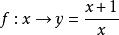 逆對應
逆對應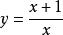 逆對應
逆對應 逆對應
逆對應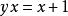 逆對應
逆對應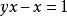 逆對應
逆對應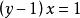 逆對應
逆對應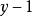 逆對應
逆對應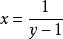 逆對應
逆對應例如,,對應法則是,這是一個從A到B的一一對應,現在要求它的逆對應的對應法則,從開始,用解方程的方法解出:方程兩端同乘x得,移項得,方程左端提取公因式得,’方程兩端同除以得,這就是逆對應的對應法則。解方程的過程中可把y看成常數,解方程的結果要得到一個用y來表達x的表達式。
對應法則相同的兩個對應不一定是同一個對應,只有在肯定一個對應是一一對應之後,才去求它的逆對應的對應法則 。