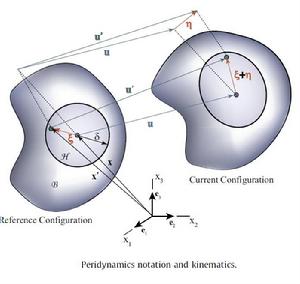
概述
近場動力學(peridynamics,PD)兼有分子動力學方法和無格線方法的優點,避免了基於連續性假設建模和求解空間微分方程的傳統巨觀方法在面臨不連續問題時的奇異性,又突破了經典分子動力學方法在計算尺度上的局限,在宏/微觀不連續力學問題分析中均表現出很高的求解精度和效率。PD方法適用於不同尺度的不連續力學問題,包括均勻與非均勻材料和結構的大變形、損傷、斷裂、衝擊、穿透和失穩問題。結晶相變動力學問題以及納米材料和結構的破壞問題。研究範圍擴展至力、電、熱、流等多物理場問題分析及其耦合分析,如:熱擴散、水力劈裂、多孔介質中的中單相流、非飽和土體中的滲流問題等;研究的材料和結構已涉及金屬、混凝土、多種複合材料和層合板結構、玻璃、顆粒材料、木材、納米纖維結構等;同時,將PD理論與現有的數值計算方法、現有理論與技術相結合也是一個有益的研究方向。
基本方程
近場動力學的基本方程如下所示。
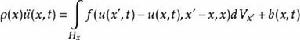 近場動力學
近場動力學 近場動力學
近場動力學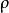 近場動力學
近場動力學 近場動力學
近場動力學 近場動力學
近場動力學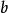 近場動力學
近場動力學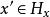 近場動力學
近場動力學 近場動力學
近場動力學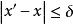 近場動力學
近場動力學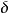 近場動力學
近場動力學其中 是計算域內的一個質點, 是物質點的密度, 是時間, 是對應質點的位移, 是物質點的體力, 是 質點的相鄰質點,滿足 ,這裡的 指的是近場範圍尺寸(稱作Horizon,由Silling定義)。
 近場動力學
近場動力學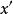 近場動力學
近場動力學 近場動力學
近場動力學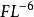 近場動力學
近場動力學向量值函式 是質點 作用在質點 上的力密度矢量,其大小取決於兩質點之間的初始相對位置以及相對位移,也必然取決於材料參數的選取,其量綱是力乘以長度的負六次方(即 ),描述的是內力與變形之間的關係。
套用
近場動力學在工程套用上的實踐還較少,亟待更多研究者的推動。