視覺特點
輻射度在繪製過程中的引入經常對最後的場景帶來更多一份的真實感，這是因為它模擬真實世界現象的方式。考慮一個在白色地板上的紅球。
光打在球上，投射出一個陰影，還有將一小部分紅光反射到周圍的物體上 - 在這個例子中，也就是地板。該現象給白色地板靠近球的地方加上了一點紅色的色調。該效應是很微妙的，但因為人類的眼睛對於其真實世界的對應現象很習慣，它可以增加真實感。
物理特點
基本的輻射度算法方法其基礎在於熱輻射的理論，因為輻射度依賴於兩個表面之間光能的傳輸。為了簡化計算，輻射度算法假設該數值在整個面片上恆定（完全或理想漫射曲面）；這意味著要計算精確的圖像，場景表述的幾何部分必須分解成更小的區域，或者說面片，然後把它們組合起來得到最後的圖像。
在這個分解之後，光能傳輸的量可以通過使用已知的反射表面的反射率和兩個面片的波形係數來計算。波形係數是一個無量綱量，它根據兩個面片的幾何朝向來計算，可以視為第一個面片所有可能發射區域的被第二個面片所覆蓋的部分所占的比例。
更精確的講，輻射度是每單位時間離開曲面片的能量，是發射和反射能量的組合：
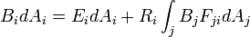輻射度算法其中:
Bi 是面片i的輻射度。
Ei 是發射的能量。
Ri 是面片的反射係數，和入射能量（從其他面片來的能量）相乘得到反射能量。
所有繪製環境中的j （j不等於i）對於BjFjidAj積分，得到離開每個面片j併到達面片i的能量。
Fji 是面片i和面片j的幾何關係決定的常數波形係數。
對偶性：
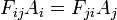輻射度算法給出：
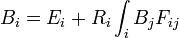輻射度算法作為簡化，積分用每個面片上恆定的輻射度取代，上式簡化為：
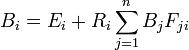輻射度算法然後該方程可以套用到每個面片。這個方程是單色的，所以彩色輻射度需要對於每個所需的色彩進行計算。
常數Fji可以用幾個計算方法。早期的方法採用半立方體 （一個假想的立方體中心位於第一個曲面，第二個曲面投影於其上，由Cohen 和Greenberg於1985年提出）以逼近波形係數，也解決了相交面片的問題。這在計算上耗費很大，因為理想的波形係數必須對一個可能的面片對導出，這導致了對於增加的幾何複雜度在計算上的二次增長。
