波色差
幾何像差
W——某一孔徑帶的光線與近軸光線的光程之差。
(D-d)法求波色差的優點[返回本章要點]
1.不需再計算F、C的實際光路;
2.校正WFC,可通過δn的改變達到,而保持nD不變
3.通過修改rk使Dk改變,可以校正殘餘的WFC
4.計算精度較高
§10-5球色差、幾何色差與波色差的關係[返回本章要點]
球色差
邊光環帶的F、C波面相交,但F、C光由於球差存在,在其它環帶波面不相交,稱球色差。
幾何色差與波色差的關係
一般光學系統:,校正色差要求:
此時
當0.707環帶相當於
校正色差
幾何色差——帶光消
波色差——邊光消,0.707帶有最大剩餘波色差,該最大值為極小。
§10-6光學系統的像差容限[返回本章要點]
像差校正到什麼程度的像差是允許的?(根據使用條件)
小像差系統(如目視光學儀器)——瑞利判據(要求)
1.色差
2.球差
①當U很小,,
②當U有一定大小,,,
(邊光不一定恰好校正到零,允許殘餘1倍焦深)
3.正弦差[返回本章要點]
以上是小視場系統容限,以下是大視場系統容限
弧矢彗差
4.像散
5.像面彎曲:在人眼調節範圍之內
6.畸變
7.倍率色差:
大像差系統(如攝影物鏡)——應校正全部像差
此時不可用瑞利判據,而要求
畸變2~4%(要求觀察者看不出像的明顯變形)[返回本章要點]
§10-7 像質評價方法
幾何像差曲線[返回本章要點]
1、球差曲線:
球差曲線縱坐標是孔徑,橫坐標是球差(色球差),使用這個曲線圖,一要注意球差的大小,二要注意曲線的形狀特別是代表幾種色光的幾條曲線之間的分開程度,如果單根曲線還可以,但是曲線間距離很大,說明系統的位置色差很嚴重。
2、軸外細光束像差曲線
這一般是由兩個曲線圖構成圖中左邊的是像散場曲曲線,右邊的是畸變,不同顏色表示不同色光,T和S分別表示子午和弧矢量,同色的T和S間的距離表示像散的大小,縱坐標為視場,右圖橫坐標是場曲,左圖是畸變的百分比值,左圖中幾種不同色曲線間距是放大色差值
焦的波差
波像差——實際波面對理想波面的偏離
軸上點A以單色光成像
存在球差,A'M交理想波面於M,
即為波差。(以理想波面為基準,右負左正)
軸上點的波像差及其與球差的關係
[返回本章要點]
球差相當的波像差為以u'2為縱坐標,以δL'為橫坐標的球差曲線與縱軸所圍面積的一半【推導】
當物方無窮遠時,u’=h/f’
討論
1.當僅有初級量時以波長為單位時,邊緣處波像差最大。移動接收面,以接收面為基準,則球差將改變,波像差曲線隨之改變。稱之為離焦
離焦,[返回本章要點]
2.當有初級和二級球差時
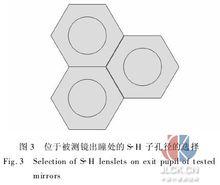 合併圖冊
合併圖冊當, 當對邊光校正球差時,0.707帶光有最大剩餘球差
若離焦,使圖中三部分面積相同,則應軸向離焦,
此時
3.若再有三級以上球差,則像差平衡的原則是:
儘可能離焦後有多個大小相等、符號相反的小面積
以下動畫是一個實際光學系統成像質量隨離焦量變化的情況[返回本章要點]
軸外點的波像差及其與垂軸像差的關係
[返回本章要點]
軸外任意一點的像差,可以用兩個分量表示
波差W應表示成與這兩個分量之間的關係
可導出
沿子午截線的波像差
推導
曲線對sinU'軸所圍的面積表征波像差的大小。參考點為高斯像點.
但高斯像點亦不一定是最佳參考點離焦
離焦
垂軸離焦:對各條光線δy'均改變同樣值。->坐標平移
沿軸離焦:縱軸轉一角度,以形成儘可能相等的大小相同、符號相反的小面積
注意
[返回本章要點]
1.垂軸離焦只為評價像質,軸向離焦才為確定最佳像面位置。
2.沿軸離焦只能對某一視場而言,不同的視場有不同的沿軸離焦要求,不能同時滿足。
3.軸向離焦中與也不能同時滿足。
應尋求最佳平衡
§10-2波像差的一般表示式[返回本章要點]
波面——等光程面,等光程面的變形——波像差。
光學系統的物方光線由y,η,ζ決定,像方光線由y',η',ζ’決定
考慮
光學系統是旋轉對稱
光束關於子午面對稱
當y=0時為軸上點
所以波差的一般表達式
式中第一行為軸向離焦與垂軸離焦項,第二行為初級單色像差引起的波像差,第三行為二級單色像差引起的波像差。
計算時應根據所取孔徑、視場大小確定應取的項
§10-3參考點移動引起的波像差,焦深[返回本章要點]
由軸向離焦:
垂軸離焦:
當光學系統為理想系統時,高斯面上波像差為零。若像面移動△l’,則可按上式計算新的W。若
則可認為該系統仍為理想系統。這時焦深為2△l'。
由上可得所以
焦深與像方孔徑有關。像方孔徑大則焦深小。
例:
§10-4色差的波像差表示[返回本章要點]