緒論
量子力學的 路徑積分表述（英語： path integral formulation）是一個從經典力學裡的作用原則延伸出來對量子物理的一種概括和公式化的方法。它以包括兩點間所有路徑的和或泛函積分而得到的量子幅來取代經典力學裡的單一路徑。
路徑積分表述的基本思想可以追溯到諾伯特·維納，他介紹的維納積分解決擴散和布朗運動的問題。在1933年他的論文中，由保羅·狄拉克把這個基本思想被擴展到量子力學中的利用拉格朗日算符。路徑積分表述是理論物理學家理察·費曼在1948年發展出來。一些早期結果是在約翰·惠勒指導下的費曼的博士論文中在早些時候已經被摸索出。
因為路徑積分的表述法顯然地把時間和空間同等處理，它成為以後理論物理學發展的重要工具之一。
路徑積分表述也把量子現像和隨機現像聯繫起來。為1970年代量子場論和概括二級相變附近序參數波動的統計場論統一奠下基礎。薛丁格方程是虛擴散係數的擴散方程，而路徑積分表述是把所有可能的隨機移動路徑加起來的方法的解析延拓。因此路徑積分表述在套用於量子力學前，已經在布朗運動和擴散問題上被套用。
數學方法
哈密頓算符
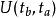路徑積分表述哈密頓算符H是量子力學中的時間演化算符 的生成算符：
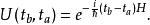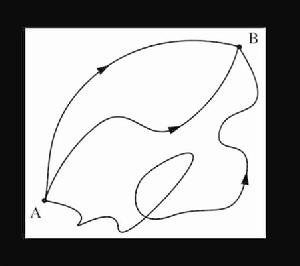
路徑積分表述一個量子粒子在時刻 t到 t間從位置x運動到x的量子機率幅是：
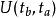路徑積分表述 路徑積分表述
路徑積分表述因為 是很複雜的算符函式，直接用以上定義計算 非常困難。 時間演化算符符合
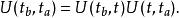路徑積分表述因此量子幅符合
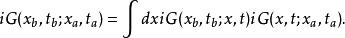路徑積分表述
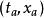路徑積分表述
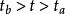路徑積分表述
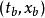路徑積分表述 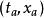路徑積分表述 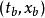路徑積分表述此公式的物理理解為：從 出發，在時刻 先穿過位置x再到達 路徑的總量子幅是兩段路徑量子幅的積；而從 到 的量子幅是所有這種路徑的和。
時間切片
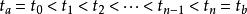路徑積分表述
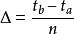路徑積分表述假設粒子在時刻t到t間從位置x運動到x。那可以把之間的時間平均分割成個別的時間區間： 。每一段的時間是 。 在時刻t和 t間粒子的量子幅是：
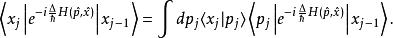路徑積分表述
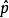路徑積分表述
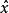路徑積分表述
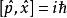路徑積分表述
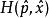路徑積分表述 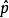路徑積分表述 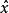路徑積分表述因為 和 是互不交換的算符，所以必須運用它們的交換子關係： 把 修成所有的 在 左方的正常順序：
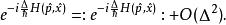路徑積分表述
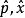路徑積分表述做時間切片的作用是：當取切片數趨向無限大的極限時，原本非正常順序的哈密頓算符可以以正常順序版代替。在正常順序算符下， 從算符簡化成普通複數。 因此
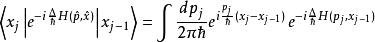路徑積分表述
路徑積分表述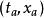 路徑積分表述 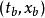路徑積分表述把所有連線 和 的路徑相加得到的總量子幅是：
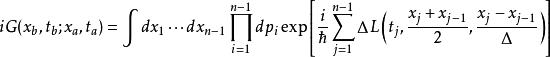路徑積分表述
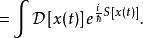路徑積分表述
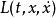路徑積分表述
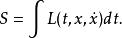路徑積分表述其中，S是路徑x(t)的作用量，拉格朗日量 的時間積分：
簡單例子
自由粒子
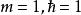路徑積分表述自由粒子的作用量（ ）：
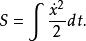路徑積分表述可以插入路徑積分里做直接計算。 暫時把指數函式內i去掉可容許比較簡易的理解計算。以後可以用威克轉動回到原式：
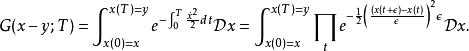路徑積分表述
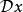路徑積分表述
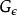路徑積分表述是以上時間切成有限片的積分。連乘里每一項都是平均值x(t)方差為c的高斯函式。多重積分是相鄰時間高斯函式 的卷積：
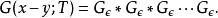路徑積分表述
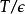路徑積分表述這裡面共包含 個卷積。傅立葉變換下卷積變成普通乘積：
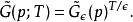路徑積分表述高斯函式的傅立葉變換也是一個高斯函式：
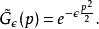路徑積分表述因此
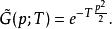路徑積分表述反傅立葉變換可以得到實空間量子幅：
路徑積分表述時間切片方法原則上不能決定以上比例係數。以隨機運動機率來理解可得到以下正規條件：
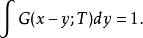路徑積分表述從這條件可得到擴散方程：
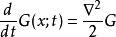路徑積分表述
路徑積分表述回到振盪軌道，即恢復分子裡的原本的i。這可同樣得到一系列高斯函式的卷積。但這些高斯積分是嚴重振盪積分而要小心計算。一個普遍方法是讓時間片帶一個小虛部。這等同於以威克轉動在實時間和虛時間間轉換。在這些處理下可得到傳播核：
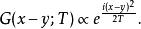路徑積分表述運用和之前一樣的正規條件，重新得到自由粒子的薛丁格方程：
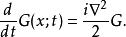路徑積分表述這意味著任何G的線性組合也符合薛丁格方程，包括以下定義的波函式：
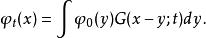路徑積分表述和G一樣服從薛丁格方程：
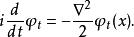路徑積分表述