距離矩陣

定義

在數學中，一個距離矩陣是一個包含一組點兩兩之間距離的矩陣(即 二維數組)。因此給定N個歐幾里得空間中的點，其距離矩陣就是一個非負實數作為元素的N×N的對稱矩陣。這些點兩兩之間點對的數量，N×(N-1)/2，也就是距離矩陣中獨立元素的數量。距離矩陣和鄰接矩陣概念相似，其區別在於後者僅包含元素（點）之間是否互相連通，並沒有包含元素（點）之間的連通的成本或者距離。因此，距離矩陣可以看成是鄰接矩陣的加權形式。

舉例闡述

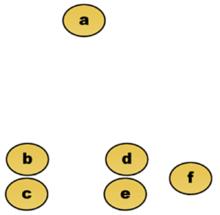
舉例來說，我們分析如下二維點a至f。在這裡，我們把點所在像素之間的歐幾里得度量作為距離度量。

距離矩陣

其距離矩陣為：

	a	b	c	d	e	f
a	0	184	222	177	216	231
b	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
e	216	128	121	46	0	83
f	231	200	203	83	83	0

解釋上矩陣：b點和c點之間的距離為45，d點與f點，e點與f點的距離相等，都為83。

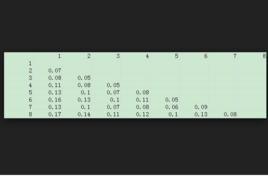
距離矩陣的這些數據可以進一步被看成是圖形表示的熱度圖（如下圖所示），其中黑色代表距離為零，白色代表最大距離。

距離矩陣

其他領域套用

在生物信息學中，距離矩陣用來表示與坐標系無關的蛋白質結構，還有序列空間中兩個序列之間的距離。這些表示被用在結構比對，序列比對，還有在核磁共振，X射線和結晶學中確定蛋白質結構。

有時候距離矩陣也被稱作相似性矩陣。