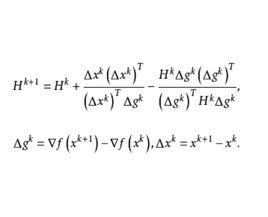基本介紹
第k+1次疊代尺度矩陣即
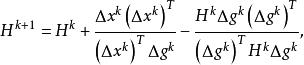尺度矩陣式中
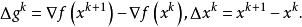尺度矩陣詳細介紹
通過放大或縮小變數的各個坐標，也就是通過變數的尺度變換可以把函式的偏心程度降到最低限度。通過尺度變換能顯著改善幾乎所有極小化方法的收斂性質。
對於二次函式
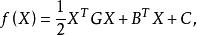尺度矩陣若進行尺度變換
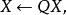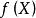尺度矩陣
尺度矩陣那么在新的坐標系中，函式的二次項將變為
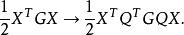尺度矩陣選擇這樣變換的目的，是為了降低二次項的偏心程度。若矩陣G是正定的，則總存在矩陣Q使
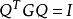尺度矩陣
尺度矩陣(其中為單位矩陣)將函式偏心度變為零。
用Q 右乘等式兩邊，得
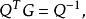尺度矩陣再用Q左乘等式兩邊，得
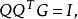尺度矩陣所以
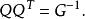尺度矩陣這說明二次函式矩陣G的逆陣，可以通過尺度變換矩陣Q來求得 。
牛頓法疊代公式為
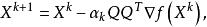尺度矩陣梯度法疊代公式為
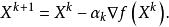尺度矩陣通過對牛頓法疊代公式和梯度法疊代公式的比較可以看出，二者的不同之處就在於牛頓法疊代公式中多了QQ 部分。QQ 實際上是在X空間內測量距離大小的一種度量，稱作 尺度矩陣，記作H，即
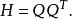尺度矩陣在進行尺度變換前，向量X長度的概念是
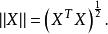尺度矩陣尺度變換後向量X對於H尺度下的長度是
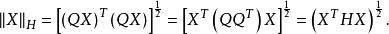尺度矩陣
尺度矩陣
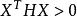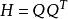尺度矩陣在這樣的長度定義下，確定“長度”這個純量大小時，使得某些方向起的作用比較大，而另一些方向起的作用比較小。為了使這種尺度有用，必須對一切非零向量X均要求，即要求尺度矩陣H正定。既然牛頓法疊代公式可用尺度變換矩陣表示出來，即
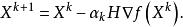尺度矩陣它和梯度法疊代公式只差一個尺度矩陣H，那么牛頓法就可看成是經過尺度變換後的梯度法。
經過尺度變換後，函式偏心率減小到零，函式的等值面變為球面(或超球面)，使設計空間中任意點處函式的梯度都通過極小點，用最速下降法只需一次疊代就可達到極小點。對變換前的二次函式，在使用牛頓方法時，由於其牛頓方向直接指向極小點，因此只需一次疊代就能找到極小點 。
