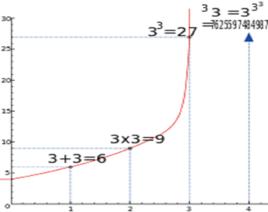
定義
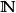 超越運算
超越運算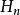 超越運算
超越運算超運算序列是定義在自然數集上的一個序列,記為。前幾項為加法(n=1)、乘法(n=2)和冪(n=3)。高階超運算的參數與冪運算相似,即a稱為底數,b稱為指數(或稱超指數),而n則稱為階數。
用高德納箭號表示法可以將超運算定義為
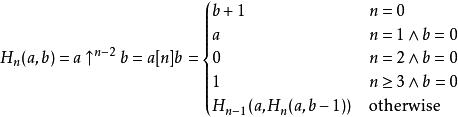 超越運算
超越運算注意到,對於序列的前三項有:
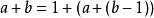 超越運算
超越運算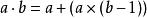 超越運算
超越運算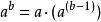 超越運算
超越運算通過這樣的遞歸能夠定義出高階運算,從而輸入很小的數就可以產生非常大的數。
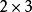 超越運算
超越運算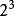 超越運算
超越運算其實,某一超運算就是一種基於低一階超運算而進行數的複合的方法。我們可以以加法、乘法與冪的概念為例來說明。加法運算就是將指定次數的1加到原本的數上從而得到最終的結果(如2+3是將1三次加到2上),乘法運算就是將指定次數的某數通加(如就是3個2相加),冪運算則是將指定次數的某數通乘(如就是3個2相乘)。
歷史
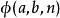 超越運算
超越運算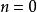 超越運算
超越運算 超越運算
超越運算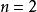 超越運算
超越運算 超越運算
超越運算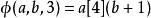 超越運算
超越運算1914年,阿爾伯特·貝內特(Albert Bennett)最早提出了超運算,他發展出了一套交換超運算(見下文)的理論。12年之後,威廉·阿克曼定義了函式,和超運算序列已經有了某種程度上的相似。最早的使用三個自變數的阿克曼函式使用了同樣的遞歸法則,但有兩點與現在的超運算不同。一是它定義了時為加法、時為乘法、時為冪運算,二是由其對初始條件的定義能得到,最後的運算結果與超運算不同。
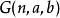 超越運算
超越運算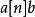 超越運算
超越運算1947年,魯賓·古德斯坦提出現在所使用的超運算序列,只是那時他使用記號來表示,而非今天的。在1947年的論文中,古德斯坦還引進了冪運算之後超運算的英文名稱,即tetration、pentation、hexation等。