簡介
超窮歸納法亦稱趙限歸納法 (transfinite induction),是數學歸納法的推廣。它是用超限歸納原理證明命題的方法。
等價形式
超限歸納原理有下列等價的形式:
1、令 P(x) 是一種性質,若 P(β) 對所有 β<α 成立蘊含 P(α) 成立,則 P(α) 對一切序數 α 都成立。即
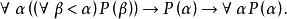 超窮歸納法
超窮歸納法2、令P(x) 是一種性質,若:
1)P(0) 成立;
2)對一切序數α,P(α) 成立蘊含 P(α+1) 成立;
3)對任何極限序數α≠0,若P(β) 對所有β<α 成立時,有P(α) 成立,則P(α) 對一切序數α 成立。即
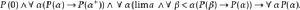 超窮歸納法
超窮歸納法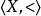 超窮歸納法
超窮歸納法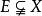 超窮歸納法
超窮歸納法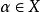 超窮歸納法
超窮歸納法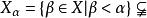 超窮歸納法
超窮歸納法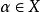 超窮歸納法
超窮歸納法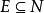 超窮歸納法
超窮歸納法3、設 E 為良序集 的歸納子集,則 E=X( 稱為歸納子集,若對任何 ,只要初始段 就有 ). 當 X 為自然數集 N 時,超限歸納法就成為數學歸納法。表述為:若 ,滿足:
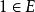 超窮歸納法
超窮歸納法1) ;
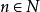 超窮歸納法
超窮歸納法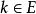 超窮歸納法
超窮歸納法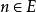 超窮歸納法
超窮歸納法2)對任何 ,若由一切小於 n 自然數 ,可推出 ,則 E=N。
數學歸納法
(Mathematical Induction, MI)
數學歸納法是一種數學證明方法,通常被用於證明某個給定命題在整個(或者局部)自然數範圍內成立。除了自然數以外,廣義上的數學歸納法也可以用於證明一般良基結構,例如:集合論中的樹。這種廣義的數學歸納法套用於數學邏輯和計算機科學領域,稱作結構歸納法。
在數論中,數學歸納法是以一種不同的方式來證明任意一個給定的情形都是正確的(第一個,第二個,第三個,一直下去概不例外)的數學定理。
雖然數學歸納法名字中有“歸納”,但是數學歸納法並非不嚴謹的歸納推理法,它屬於完全嚴謹的演繹推理法。事實上,所有數學證明都是演繹法。
