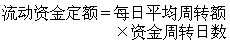定義
質點運動微分方程是用牛頓第二定律描述質點運動的微分方程。
方程
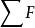質點運動微分方程設質量為m的質點Q，在F，F，…，F諸力的作用下運動。若以a表示質點的加速度，以表示諸力的合力（見圖），則由牛頓第二定律有：
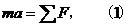質點運動微分方程或寫成：
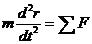質點運動微分方程式中r為質點的矢徑，這是矢量形式的質點運動微分方程。
把式（1）在直角坐標軸上投影，得：
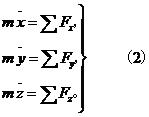質點運動微分方程這是直角坐標軸投影形式的質點運動微分方程。
若把式（1）投影到圖中的（t、n、b）自然坐標軸上，則有：
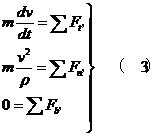質點運動微分方程
質點運動微分方程式中ρ是質點在其軌跡上所在點的曲率半徑。式（3）是自然坐標軸投影形式的質點運動微分方程。從（3）可以看出，作半徑為R的勻速圓周運動的質點，只受向心力作用，其值為，其中v為速率。
以上各種形式的質點運動微分方程都建立了質點的運動與作用力之間的關係。知其一就能求出其二，因此，套用它可以解決兩類問題：
①第一類質點動力學問題已知質點的運動規律，求質點上的作用力。設已知質點在直角坐標中的運動方程為：
x=x（t），
y=y（t），
z=z（t），
將其對時間微分兩次，套用式（2）可得質點上的作用力的三個分力。
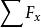質點運動微分方程
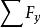質點運動微分方程
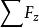質點運動微分方程②第二類質點動力學問題已知質點上所受的力，求質點的運動規律，即從質點運動微分方程通過積分求解質點的運動方程。在一般情況下，質點上所受的力既可能是常力，也可能是隨時間、速度，位置而變化的變力。因此，、、是t、x、y、z、x、y、z的函式。於是式（2）有以下形式：
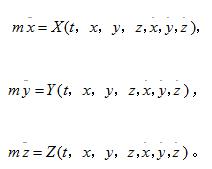質點運動微分方程這是三個二階微分方程，積分後將得到包含六個積分常數的解，即
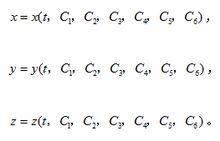質點運動微分方程上式中六個積分常數要由質點運動的初始條件來確定。這個初始條件就是質點的初始位置和初始速度。當t=0時，初始位置為x=x，y=y，z=z；初始速度為v=x，v=y，v=z。在解決具體問理時，必須知道初始條件，才能得到確定的解答。
在動力學中還有一些問題是這兩類問題的綜合。
