定義
 變質量體運動
變質量體運動變質量體是在運動過程中本身質量發生明顯變化的物體,這種物體的運動就是變質量體運動。這裡所說的物體質量的變化不是指質量的消滅或產生,而是指在某一瞬時以前或以後,物體中有一部分質量未被考慮在內;前者相當於有質量併入而使物體的質量增加,後者相當於有質量分出而使物體的質量減少。如果變質量體的轉動速度和加速度同平動的速度和加速度相比可以忽略不計,則此變質量體可看作一個變質量點。這種情況下的變質量體問題仍屬經典力學範疇。
例子
在工程技術和自然界中有許多變質量體的例子:火箭噴出燃料燃燒後的殘餘物使火箭質量發生變化;噴氣飛機是一般情況下的變質量體,它不斷吸入空氣而使質量增加,但又不斷噴出燃氣而使質量減少,即質量的併入和分出同時發生;流星體在闖入大氣層時,質量由於摩擦燃燒而減少;浮冰由於海水凍結使質量增加,或由於融化而使質量減小;棉紡廠的紗錠在轉動過程中也在不斷改變質量和轉動慣量,等等。
物理解釋
基本運動微分方程 假設變質量質點的併入或分出微粒是連續發生的,而且這種質量的併入或分出是屬於微粒和質點的接觸作用,即微粒和質點併入或分出時發生碰撞而產生微粒速度的突變,從而使質點的速度發生連續的變化;併入或分出以後,作用也就停止。
牛頓第二定律原來只用於常質量物體的運動,但如在兩個瞬時考察相同總質量的動量變化,也可用於變質量物體的運動。
設變質量質點的質量m是時間t的函式,即m=m(t)。在瞬時t,質點的質量為m(t),質點對於定坐標系Oxyz的速度為v
即將與之合併的微粒的質量為dm(t),其對Oxyz的速度為u。在瞬時t+dt,微粒與質點合併。於是質點的質量變為(m+dm),其對Oxyz的速度成為v+dv。對於質量分出的情況(如火箭),則dm<0,即為負。 m和dm所組成的質點系在瞬時t的動量為mv+udm;在瞬時t+dt的動量為(m+dm)(v+dv)。在dt時間內,動量的增加dp為:
dp=(m+dm)(v+dv)-(mv+udm)。
這是變質量質點的基本運動微分方程的另一種形式,是俄國И.В.密歇爾斯基於1897年導出的,稱為密歇爾斯基方程。式中F為外力;Φ具有力的量綱,稱為反推力。
變質量質點的速度同初始質量m0對剩餘質量m的比值有關。在v0=0的條件下,設噴射終了時質點的質量為ms(此即燃料燒完時火箭殼體的質量),燃料的質量為mf,則火箭在噴射終了時的速度 v1可求得:
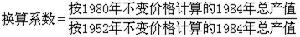
此式稱為齊奧爾科夫斯基公式。К.Э.齊奧爾科夫斯基是開拓火箭技術領域的先驅者之一。
推出如下結論:① v1與相對速度成正比;②m0/ms或mf/ms越大,則v1越大;③v1與噴射規律f(t)無關,即與燃料的快慢無關(這是不考慮Fx的結果);④如要提高v1,提高vr比增加m0/ms更為有效。
這就是變質量質點的動量定理。
d(mv)=Fdt+Rdt,
就得到變質量質點的衝量定理:變質量質點動量的微分,等於外力的元衝量和微粒絕對運動引起的反推力元衝量之和。
變質量質點的動量矩定理 變質量質點對某固定點的動量矩定義為r×mv,式中r為由固定點引出的矢徑。
變質量質點對某一固定點的動量矩的時間導數,等於外力和微粒絕對運動引起的反推力合力對同一固定點之矩。
將變質量質點的基本方程的兩邊各項分別點乘以vdt或dr,移項後得:
mv·dv+v·vdm=F·dr+v·udm,
此外,是反推力,兩邊點乘以v,移項後得:
v·u dm=Φ·dr+v2dm。
這就是變質量質點的動能定理:變質量質點動能的微分,等於所有外力的元功、反推力的元功和噴出微粒的元質量由於牽連速度而產生的動能之代數和。
參考書目
.В.□ещерский,Рабо□ыпомеханике□елпеременноймассы,Изд.2-e,Гостехиздaт,□осква,1952.
.□.Карагодин,Теоре□ическиеосновымеханики□елапеременногосос□ава,Оборонгиз,□осква,1963.
(黃克累)