基本介紹
定義
資本市場線可表達為:
總報酬率=Q*(風險組合的期望報酬率)+(1-Q)*(無風險利率)
其中 :Q代表投資者自有資本總額中投資於風險組合M的比例,1-Q代表投資於無風險組合的比例。
雖然資本市場線表示的是風險和收益之間的關係,但是這種關係也決定了證券的價格。因為資本市場線是證券有效組合條件下的風險與收益的均衡,如果脫離了這一均衡,則就會在資本市場線之外,形成另一種風險與收益的對應關係。這時,要么風險的報酬偏高,這類證券就會成為市場上的搶手貨,造成該證券的價格上漲,投資於該證券的報酬最終會降低下來。要么會造成風險的報酬偏低,這類證券在市場上就會成為市場上投資者大量拋售的目標,造成該證券的價格下跌,投資於該證券的報酬最終會提高。經過一段時間後,所有證券的風險和收益最終會落到資本市場線上來,達到均衡狀態。
介紹
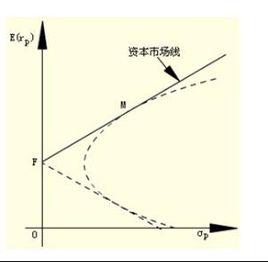
在資本資產定價模型假設下,當市場達到均衡時,市場組合成為一個有效組合,而所有有效組合都可視為無風險資產與市場組合的再組合;這些有效組合在期望收益率和標準差的坐標系中剛好構成連線無風險資產F與市場組合M的射線FMH,這條射線稱為資本市場線。
表達式
資本市場線中,縱坐標是總期望報酬率、橫坐標是總標準差
根據:總期望報酬率=Q×風險組合的期望報酬率+(1-Q)×無風險利率
總標準差=Q×風險組合的標準差
可知:
當Q=1時,總期望報酬率=風險組合的期望報酬率,總標準差=風險組合的標準差
當Q=0時,總期望報酬率=無風險利率,總標準差=0
所以,資本市場線的斜率=(風險組合的期望報酬率-無風險利率)/風險組合的標準差
由於資本市場線中,截距為無風險利率,所以,資本市場線的表達式應該為:總期望報酬率=無風險利率+[(風險組合的期望報酬率-無風險利率)/風險組合的標準差]×總標準差。或者表述為:投資組合的期望報酬率=無風險利率+[(風險組合的期望報酬率-無風險利率)/風險組合的標準差]×投資組合的標準差.
經濟意義
資本市場線公式對有效組合的期望收益率和風險之間的關係提供了十分完整的闡述。有效組合的期望收益率由兩部分構成:一部分是無風險利率,它是由時間創造的,是對放棄即期消費的補償;另一部分則是[E(rM-rF)σP]/σM,是對承擔風瞼的補償,通常稱為“風險溢價”,與承擔的風險的大小成正比。其中的係數[E(rM-rF)]/σM代表了對單位風險的補償,通常稱之為風險的價格。
與SML區別
(1)“資本市場線”的橫軸是“標準差(既包括系統風險又包括非系統風險)”,“證券市場線”的橫軸是“貝塔係數(只包括系統風險)”;
(2)“資本市場線”揭示的是“持有不同比例的無風險資產和市場組合情況下”風險和報酬的權衡關係;“證券市場線”揭示的是“證券的本身的風險和報酬”之間的對應關係;
(3)“資本市場線”中的x軸“Q”不是證券市場線中的“貝塔係數”,資本市場線中y軸“風險組合的期望報酬率”與證券市場線的“平均股票的要求收益率”含義不同;
(4)資本市場線表示的是“期望報酬率”,即投資“後”期望獲得的報酬率;而證券市場線表示的是“要求收益率”,即投資“前”要求得到的最低收益率;
(5)證券市場線的作用在於根據“必要報酬率”,利用股票估價模型,計算股票的內在價值;資本市場線的作用在於確定投資組合的比例。
(7)SML與CML都可描述風險與收益的關係,但是CML中的風險指總風險,SML中的風險則是系統性風險。
(8)SML無論對單個證券或證券組合都適用,CML只適用於有效組合。