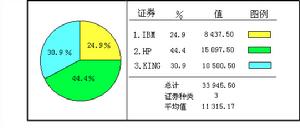
 證券組合分析圖
證券組合分析圖(一)兩種證券組合的收益和風險
設有兩種證券A和B,某投資者將一筆資金以x的比例投資於證券A,以y的比例投資於證券B,且x+y=1,稱該投資者擁有一個證券組合P。如果到期時,證券A的收益率為a,證券B的收益率為b,則證券組合P的收益率Q為:
Q=ax+by
證券組合中的權數可以為負,比如x<0,則表示該組合賣空了證券A,並將所得的資金連同自有資金買入證券B,因為x+y=1,故有y=1-x>1。
投資者在進行投資決策時並不知道x和y的確切值,因而x、y應為隨機變數,對其分布的簡化描述是它們的期望值和方差。投資組合P的期望收益率E和收益率的方差為:
E=xa+yb
方差=x的平方×證券A的方差+y的平方×證券B的方差+2xy×證券A的標準差×證券B的標準差×證券組合的相關係數
式中:
證券A的標準差×證券B的標準差×證券組合的相關係數——協方差,記為COV(A,B)
舉例說明:
已知證券組合P是由證券A和B構成,證券A和B的期望收益、標準差以及相關係數如下:
證券名稱 期望收益率 標準差 相關係數 投資比重
A 10% 6% 0.12 30%
B 5% 2% 0.12 70%
那么,組合P的期望收益為:
期望收益=( 0.1 × 0.3 + 0.05 × 0.7 ) × 100% = 6.5%
組合P的方差為:
方差=( 0.3 × 0.3 × 0.06 × 0.06 ) + ( 0.7 × 0.7 × 0.02 × 0.02 ) + ( 2 × 0.3 × 0.7 × 0.06 × 0.02 × 0.12 ) = 0.0327
選擇不同的組合權數,可以得到包含證券A和證券B的不同的證券組合,從而得到不同的期望收益率和方差。投資者可以根據自己對收益率和方差(風險)的偏好,選擇自己最滿意的組合。
(二)多種證券組合的收益和風險
這裡將把兩個證券的組合討論拓展到任意多個證券的情形。設有N種證券,記作 A1 、A2 、A3 、… 、AN ,證券組合P = ( x1 ,x2 ,x3 ,… ,xn ) 表示將資金分別以權數 x1 、x2 、x3 、…、xn,投資於證券 A1 、A2 、A3 、… 、AN 。如果允許賣空,則權數可以為負,負的權數表示賣空證券占總資金的比例。正如兩種證券的投資組合情形一樣,證券組合的收益率等於各單個證券的收益率的加權平均。即:設Ai的收益率為Ri ( i = 1 ,2 ,3 ,…,N ) ,則證券組合P = ( x1 ,x2 ,x3 ,… ,xn ) 的收益率為:
Rp = x1 × r1 + x2 × r2 + … + xn × rn = ∑xi ri
推導可得證券組合P的期望收益率和方差為:
E ( rp ) = ∑xi E(ri) ( 1 )
方差 = ∑i∑j xi XJ cov(xi , xj) ( 2 )
由式( 1 )和( 2 )可知,要估計E(rp) 和 方差,當N非常大時,計算量十分巨大。在計算機技術尚不發達的20世紀50年代,證券組合理論不可能運用於大規模市場,只有在不同種類的資產間,如股票、債券、銀行存單之間分配資金時,才可能運用這一理論。20世紀60年代後,威廉·夏普提出了指數模型以簡化計算。隨著計算機技術的發展,以開發出計算E(rp) 和 方差的計算機運用軟體,如:Matlab 、SPSS 和 Eviews 等,大大方便了投資者。
