解集[數學用語]

解集是一個數學用語，指以一個方程（組）或不等式（組）的所有解為元素的集合叫做該方程（組）或不等式（組）的解集。表示解的集合的方法有三種：列舉法、描述法和圖示法。解集作為數學中的重要工具，在數學中有著十分廣泛的套用。

基本信息

• 中文名：解集
• 定義：方程解的集合

• 套用學科：數學
• 適用領域範圍：代數
• 性 質：數學用語
• 表達方式：列舉、描述、圖示

定義

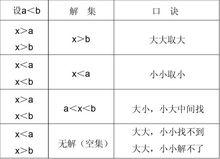尋找解集的方法

以一個方程（組）或不等式（組）的所有解為元素的集合叫做該方程（組）或不等式（組）的解集。解集作為數學中的重要工具，在數學中有著十分廣泛的套用。很多題的結論均需用解集表示。

例：

x^2-1≥0的解集就是X={x|x≤-1，x≥1}；

x^2-1≤0的解集就是X={x|-1≤x≤1}；

x^2-3x-4=0的解集是X={-1,4}。

性質

方程（組）或不等式（組）的所有解均在其解集中，解集中的所有元素均為方程（組）或不等式（組）的解。無解的方程（組）或不等式（組）的解集為空集。

線性代數裡向量（或矩陣）方程的解集是向量（或矩陣），這類元素構成集合，就不能稱為區間或區域了。

函式方程（微分方程和積分方程）的解集是函式，解集裡的元素都是函式。

對於二元不等式（組）的解集就是一個平面區域。

解集的表示法

解集的表示法也即集合的表示法，就是給出一個集合和組成這個集合的元素的表示方法。表示集合的方法有三種。

列舉法

列舉法，又叫外延法。把集合的元素一一列舉出來，寫在大括弧“{ }”內，並用逗號“，”把它們彼此分開。例如，小於10的素數集合A可表示為A={2,3,5,7}。又如3的自然數冪所組成的集合B可表示為B={3,9,27,…,3 ,…}。在用列舉法表示一個無限集或元素很多的集的時候常用省略號。這時，要注意表示的明確性，要能從已經列舉的元素中知道被省略的元素是什麼。在用列舉法表示集合時，元素的次序無關緊要，但不允許重複。

描述法

描述法，又稱特徵性質法或內涵法。利用概括原則指出確定集合元素的特徵性質P(x)，從而給出集合的方法稱為描述法。具有性質P(x)的所有元素 x 組成的集合A記為A={x|P(x)}或{x：P(x)}。其中P{x}表示集合中元素的特徵性質。所謂集合元素的特徵性質是指：集合的每個元素的共有的性質，並且不屬於這個集合的元素都不具有這個性質。

圖示法

解集[數學用語]

圖示法，如維恩圖法。用圓、橢圓、矩形或其他封閉曲線圍成的區域表示集合。如右圖所示，矩形表示全集I，曲線包圍的區域表示集合A，B，C等。這種方法嚴格地說應稱示意法，有一定的局限性，但它的直觀性能幫助人們思考。

特殊集合的習慣表示法，如常以字母N，Z，Q，R，C分別表示自然數集、整數集、有理數集、實數集、複數集等。在數學的各分支中，也有用約定的特殊符號（或特殊圖形）來表示特定集合的。