簡介
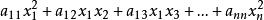西爾維斯特慣性定理
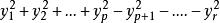西爾維斯特慣性定理
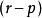西爾維斯特慣性定理
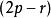西爾維斯特慣性定理在代數學中， 西爾維斯特慣性定理（Sylvester's law of inertia）是指在實數域中，一個形如的二次型通過線性變換可以化簡成惟一的標準型。其中的正項數（稱為正慣性係數）、負項數（稱為負慣性係數）以及 0 的數目惟一確定，其中的r為係數矩陣的秩。正慣性係數p－負慣性係數的值稱作符號差。
線性映射
在數學中， 線性映射（有的書上將“ 線性變換”作為其同義詞，有的則不然）是在兩個向量空間（包括由函式構成的抽象的向量空間）之間的一種保持向量加法和標量乘法的特殊映射。線性映射從抽象代數角度看是向量空間的同態，從範疇論角度看是在給定的域上的向量空間所構成的範疇中的態射。
“線性運算元”也是與“線性映射”有關的概念。但是不同數學書籍上對“線性運算元”的定義存在區別。在泛函分析中，“線性運算元”一般被當做“線性映射”的同義詞。而有的書則將“線性運算元”定義為“線性映射”的自同態子類。
二次型
在數學中， 二次型是一些變數上的二次齊次多項式。例如
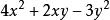西爾維斯特慣性定理是關於變數x和y的二次型。
二次型在許多數學分支，包括數論、線性代數、群論(正交群)、微分幾何(黎曼測度)、微分拓撲(intersection forms of four-manifolds)和李代數(基靈型)中，占有核心地位。
參見
•二次形式 (統計)
