計算方法
複利到期收益率的計算方法為：
設：r=複利到期收益率；C=年利息(年利率×面額)；P=購買價格(投資本金)；m=每年付息次數；n=距到期年數；R=債券面額
當m=1時(即當債券每年付息一次時)：
假如以價格P買人某種債券後按複利方式計算，則一年後債券的價值為：
p1 = p + pr = p(1 + r)
複利到期收益率二年後，債券的價值為：
n年後，債券的價值為：
pn = p(1 + r)n ……………………………………………………(1)
再假如該債券的年利息為C，以複利方式計算，則一年後可得到利息C，二年後可得利息C+C(1+r)，三年後可得利息C + C(1 + r) + C(1 + r)^2 ，
n年後可得利息C + C(1 + r) + C(1 + r)^2 + C(1 + r)^3 +……C(1 + r)^(n - 1) 。
因此，當n年後償還時，該債券的價值應為利息與面額之和：
pn = C(1 + r)n -1 + C(1 + r)n - 2 +…C + R ………(2)
複利到期收益率用等比級數前n項和的公式將(2)式整理後：
通過(1)式和(3)式，可以引出：
p(1 + r)n = C / r[(1 + r)n -1] + R……………………………(4)
通過(4)式，可以求出購買價格：
P = C / r[(1 + r)n -1) / (1 + r)n + [R / (1 + r)n] ……………………(5)
在(5)式中，r就是複利到期收益率，P是包括應計利息的價格。因從(4)式和(5)式無法直接求出複利到期收益率r，所以通常使用固定程式的電子計算機求近似值。
(5)式用文字表示為：
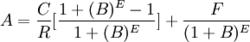複利到期收益率市場價格=C
其中：A為市場價格；B為收益率；E為距到期年數；F為面額
上式中的收益率系指複利到期收益率。
相關條目
單利到期收益率
參考文獻
1 王兆星,吳國祥,陳世河.金融市場學（第三版）.中國金融出版社,2004年02月第1版.
