基本介紹
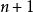 升階法
升階法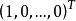 升階法
升階法行列式計算的一般方法是降階,但對於某些特殊的n階行列武,如除對角元素(或次對角元素)外,其餘元素相同或成比例的行列式。有時加上一行一列變成階的行列式,特別是第1列為並適當選擇第1行的元素,就可以使消零化筒更方便,且化簡後常變成箭形行列式。這一方法稱為 升階法或 加邊法 。
例題解析
【例1】計算n階行列式
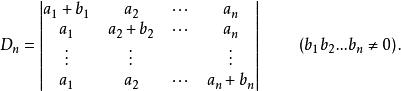 升階法
升階法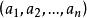 升階法
升階法分析: 該行列式除對角元之處。各行的元素均為。
【解】(先升階)
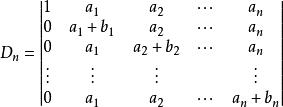 升階法
升階法 升階法
升階法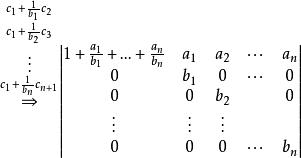 升階法
升階法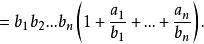 升階法
升階法
計算行列式通常用降階法,但有時也可反其道而行之,將它的階數放大,增加一行一列,使升階後的行列式與原行列式相等,且易於計算(即適當選擇所增加的行列元素,使下一步化簡後出現大量的零元素),這種方法叫做升階法或加邊法。它的理論依據是行列式依行(列)展開定理。通常在行列式各行(列)中相同元素較多時,可考慮利用加邊法 。
 升階法
升階法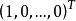 升階法
升階法行列式計算的一般方法是降階,但對於某些特殊的n階行列武,如除對角元素(或次對角元素)外,其餘元素相同或成比例的行列式。有時加上一行一列變成階的行列式,特別是第1列為並適當選擇第1行的元素,就可以使消零化筒更方便,且化簡後常變成箭形行列式。這一方法稱為 升階法或 加邊法 。
【例1】計算n階行列式
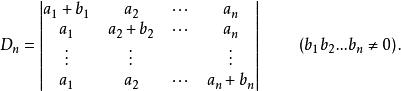 升階法
升階法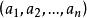 升階法
升階法分析: 該行列式除對角元之處。各行的元素均為。
【解】(先升階)
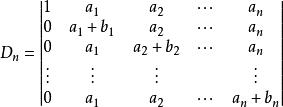 升階法
升階法 升階法
升階法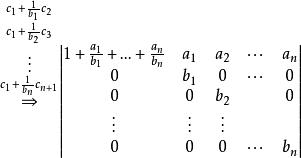 升階法
升階法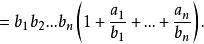 升階法
升階法光屬性·魔法師族No.104 光屬性·戰士族No.10 裁斷魔王、CNo.96
卡片信息 調整信息 升階變化 動畫信息階躍法的實質是將在系統中作定常流動的流體切換為流量相同的含有示蹤劑的流體,或者相反。前一種做法稱為升階法(或稱正階躍法),後一種則叫降階法(成稱負階躍法...
「觀測結果」的習慣。 星光 埃利法斯 聲優:浜田賢二 卡組:升階向...世界。他們以讓超量怪獸混沌化的「RUM(升階魔法)」為王牌,阻擋在游馬...為了追求“更進一步的升階”而創造出來的神。只以星光世界的理想為目標,視混沌...
故事簡介 角色介紹 製作人員 相關設定 No.卡世界。他們以讓超量怪獸混沌化的“RUM(升階魔法)”為王牌,阻擋在游馬...
劇情簡介 角色介紹 設定解說 登場No.卡 製作人員《獸法狂暴》,作者靈山悍匪,是一部異界大陸類的網路連載小說作品。
網路小說《獸法狂暴》 《獸法狂暴》初章 《獸法狂暴》目錄襲上手難度:5星遠程法術型職業,射程遠、範圍廣,以玲瓏多變的千幻術法...升階界面,可對神將進行升階和自動升階操作,點擊一鍵升階後系統會一直升階直到成功升階或用完升階道具。升階消耗對應的神將碎片,進度條是幸運值...
遊戲簡介 職業介紹 遊戲系統、孤傲,寡言少語,眉宇間隱隱透出一絲的邪氣。修煉法杖類武器,講究杖、法合一...三國》常見問題武器界面我有兩把相同名字的兵器,為什麼不能升階? A:您在兵器庫中看到的都是現有兵器,而背包中的則是兵器卡牌。兵器升階必須是一把現有...
基本信息 遊戲特色 四大職業介紹 《Q將三國》武將 《Q將三國》職業加點攻略在神將功能中升階時的生命值:呂布、風逸、弓凌、嵇康、赤慣妖魔、萬妖皇。4...邂逅千城雪,面見仙法高深的太白真人,得知仙魔世界逐漸出現了異象,似有大事...升階兩儀石:用於二星綠色品質夥伴升階三才寶珠:用於三星藍色品質夥伴升階...
遊戲介紹 遊戲配置 遊戲截圖 開服信息 版本更新丐幫絕學降龍十八掌 出自丐幫洪七公的曠世武學,降龍十八掌與打狗棍法並稱...功能,對裝備進行強化、升階、洗鍊品質、洗鍊類型、洗鍊數值。鐵匠會親自為您...、BOSS掉落、活動中獲取。裝備升階裝備升階可提讓裝備提升到更高等階的裝備...
遊戲設定 遊戲特色 特色系統 升級攻略