螺旋面[幾何曲面]

一條母線繞著一條軸線作螺旋運動（等速旋轉和等速軸向移動）而形成的曲面，稱為螺旋面（Helicoidal Surface）。常見的螺旋面有正螺旋面、斜螺旋面（阿基米德螺旋面）、sincos螺旋面、漸開螺旋面等。與螺旋線一樣，螺旋面也有右旋與左旋之分。

介紹

螺旋面[幾何曲面]

螺旋面是一類常見的曲面。以螺旋線和它的軸線為導線，直母線(也可以是曲母線)沿兩條導線滑動，並始終與軸線交成定角所形成的曲面稱為螺旋面。同螺旋線一樣，螺旋面也分成左旋和右旋兩種。在形成螺旋面的過程中，母線上各點軌跡都是螺旋線。這些螺旋線導程相等。畫出螺旋線和軸線的投影，再畫出若干直素線的投影以及包絡線，就得到螺旋面的投影。 常見的螺旋面有正螺旋面、斜螺旋面（阿基米德螺旋面）、sincos螺旋面、漸開螺旋面等。

正螺旋面

圖1

直線與軸線正交時所形成的螺旋面稱為“正螺旋面”。正螺旋面就是讓一條直線L的初始位置與X軸重合，然後讓直線L一邊繞Z軸作勻速轉動，一邊沿z軸方向作勻速運動，則直線在這兩種運動的合成下掃出的曲面就是正螺旋面。顯然正螺旋面可以看做是由直線形成的，即它是一個直紋面。

使用WHY數學圖形可視化工具編程，其程式示例如下，得到的螺旋面如圖1所示。

vertices = D1:32 D2:360u = from 0 to 3 D1

v = from 0 to (8*PI) D2

x = u*cos(v)

y = v*0.5z = u*sin(v)

斜螺旋面

圖2

直線與軸線斜交時所形成的螺旋面稱為“斜螺旋面”。以一條與軸線成定角相交的直線為母線，繞軸線做螺旋運動運動所形成的曲面，稱為斜螺旋面。實質上，阿基米德螺旋面就是正螺旋面變化了下高度參數。使用WHY數學圖形可視化工具編程，其程式示例如下，得到的螺旋面如圖2所示。

vertices = D1:100 D2:360u = from 0 to (2) D1

v = from 0 to (8*PI) D2

x = -u/SQRT2*cos(v)

y = u/SQRT2 + v/PI/2z = -u/SQRT2*sin(v)

漸開線螺旋面

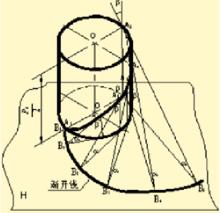圖3

直母線作螺旋運動的同時，且與導圓柱面上的螺旋線相切形成的曲面稱為漸開線螺旋面。如圖 3中直母線AB繞軸線OO作螺旋運動，同時與導圓柱面上的螺旋線相切（切點為A 0 、A 1 、A 2、 …、A 5 ），則母線AB在空間形成了漸開線螺旋面。漸開線的螺旋面的直母線與導圓柱面上的素線夾角等於螺旋線的螺旋角，而螺旋升角+螺旋角=90°，如果已知導圓柱直徑 d、 螺旋面導程 Ph 和直母線長L，既可繪製出漸開線螺旋面的投影圖。

漸開線螺旋面的兩個基本性質為：① 它與正截面相交所得交線為一漸開線。② 漸開線螺旋面的直母線上任一點的運動軌跡為與曲導線具有相同導程的圓柱螺旋線。

使用WHY數學圖形可視化工具編程，其程式示例如下，得到的螺旋面如圖4所示。

圖4

vertices = D1:100 D2:360u = from 0 to (4*PI) D1

v = from 0 to (8*PI) D2

x = 2*[cos(u+v) + u*sin(u+v)]

y = v

z = 2*[sin(u+v) - u*cos(u+v)]