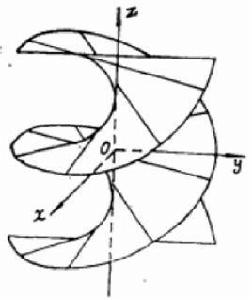
螺旋面
正螺面螺旋面是一類常見的曲面。以螺旋線和它的軸線為導線，直母線(也可以是曲母線)沿兩條導線滑動，並始終與軸線交成定角所形成的曲面稱為螺旋面。同螺旋線一樣，螺旋面也分成左旋和右旋兩種。在形成螺旋面的過程中，母線上各點軌跡都是螺旋線。這些螺旋線導程相等。畫出螺旋線和軸線的投影，再畫出若干直素線的投影以及包絡線，就得到螺旋面的投影 。常見的螺旋面有正螺旋面、斜螺旋面（阿基米德螺旋面）、sincos螺旋面、漸開螺旋面等。
正螺面定義
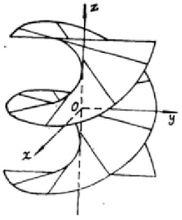圖1正螺面的圖形如圖1所示。
定義1：由一條垂直於螺旋軸的直線作螺旋運動時所畫出的曲面叫正螺面。
旋轉是以定角速度 w順著 z軸方向，且移動的距離與轉角 v 與( x 軸交角 ) 成正比，即正螺面的母線與螺線的“軸”垂直相交，當交點N沿軸移動時，母線繞軸旋轉，且N點轉動的距離與母線轉動的角度成正比。把 z 軸取作旋轉軸，M點為正螺面上任意一點，MN垂直於z軸，設MN=u，OP為MN在xy平面上的投影，OP與 x 軸的交角為 v 。 a 表示螺距 ( 比例係數 ) ，則正螺面的方程可寫成：
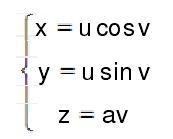正螺面即：
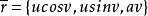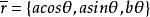正螺面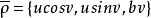
正螺面
正螺面定義2：圓柱螺線 的主法線曲面（直紋面）為正螺面 。
性質
正螺面是經典微分幾何曲面論中的重要研究對象，本身具有很多重要的幾何性質，例如正螺面是一種特殊的直紋面，可看作圓柱螺線的主法線面；正螺面的平均曲率恆為零，因此是極小曲面；此外通過計算正螺面的Gauss曲率，可以發現其Gauss曲率沿著直母線的正交軌線保持不變。
定理1：設α是一條曲率和撓率均恆不為零的曲線，S為α的主法線面。如果S沿著每條直母線平均曲率保持不變，則S必為正螺面。
定理2：設α是一條曲率和撓率均恆不為零的曲線，S為α的主法線面。如果S沿著每條直母線的正交軌線Gauss曲率保持不變，則S必為正螺面。
由定理1可直接得到如下推論：
推論：設S為某條曲率和撓率均恆不為零的曲線的主法線面。如果S的平均曲率為常數，則S必為正螺面 。
正螺面的性質
（1）正螺面的坐標曲線網是正交曲線網、漸近曲線網和等溫網；
（2）正螺面的直紋性：正螺面是直紋曲面，但不可展；
（3）正螺面是極小曲面：正螺面上的任意光滑曲線C圍成的曲面區域最小，換句話說，正螺面是極小曲面。
