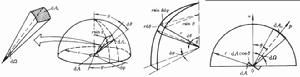
簡介
用史蒂芬-波爾茲曼定律,只能計算絕對黑體表面所輻射的總能量,而並不能說明在半球空間各個方向上發射的輻射能量是如何分布的。蘭貝特定律則定量地描述了這一分布規律,即黑體表面向它上面的半球空間給定方向上發射的輻射能量,等於它向法線方向上發射的輻射能量與給定方向和法線方向夾角的餘弦的乘積。
定理內容
蘭貝特定律——定向輻射強度與方向無關。給出了黑體輻能按空間分布的規律。
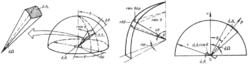 蘭貝特定律
蘭貝特定律公式表示:L(θ)=L=常數
推導
蘭貝特定律是描述黑體輻射能量隨空間(方向)分布規律的定律,其具體內容如下黑體表面向θ方向發射的定向輻射力:
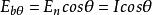 蘭貝特定律
蘭貝特定律式中為發射輻射的方向θ與表面法線的夾角;E為黑體表面向θ方向發射的定向輻射力;E為黑體表面法線方向上的定向輻射力,其值最大;I為黑體表面θ方向上的輻射亮度;I為黑體表面法線方向上的輻射亮度。在此處,因黑體向各方向發射的輻射亮度均相等,故:I=I=I由定義可知E=I,於是Icosθ=E。
對2n空間求積分可得:
E=Iπ
上式表明,黑體表面輻射能量隨空間(方向)分布遵循餘弦規律,即表面法線方向上輻射能量值最大,切線方向上為零,其餘方向由cos決定,故蘭貝特定律又稱餘弦定律。
套用
一般地講,對於一個表面的輻射模型,蘭貝特定律是十分近似的。如果一個表面嚴格遵循蘭貝特定律,則相對於此表面任何一個角度上所測得的輻射流,都可用來計算其總的球向輻射流。
在半球空間的各個方向上,輻射亮度I均相等的表面,稱為漫輻射面,也稱為各向同性表面,故對漫輻射面而言,蘭貝特定律成立。