定義
蘭徹斯特方程是描述交戰過程中雙方兵力變化關係的微分方程組。
發展史
因系F.W.蘭徹斯特所創，故有其名。1914年，英國工程師蘭徹斯特在英國《工程》雜誌上發表的一系列論文中，首次從古代使用冷兵器進行戰鬥和近代運用槍炮進行戰鬥的不同特點出發，在一些簡化假設的前提下，建立了相應的微分方程組，深刻地揭示了交戰過程中雙方戰鬥單位數（亦稱兵力）變化的數量關係。
第二次世界大戰後，各國軍事運籌學工作者根據實際作戰的情況，從不同角度對蘭徹斯特方程進行了研究與擴展，使蘭徹斯特型方程成為軍事運籌學的重要基本理論之一。有些學者也將蘭徹斯特型方程稱為蘭徹斯特戰鬥理論或戰鬥動態理論。蘭徹斯特型方程與計算機作戰模擬結合以後所構成的各種形式、各種規模的作戰模型，在軍事決策的各有關領域中得到了廣泛的套用。
主要形式
平方律
蘭徹斯特方程設在近代戰鬥條件下，紅、藍兩軍交戰，雙方各自裝備同類武器，相互通視，並在武器射程範圍內進行直接瞄準射擊；雙方每一戰鬥單位射擊對方每一戰鬥單位的機會大致相同。將雙方在戰鬥中尚存的戰鬥單位數作為連續的狀態變數，以m(t)、n(t)表示在戰鬥開始後t時刻藍方、紅方在戰鬥中尚存的作戰單位數，可用下列微分方程組來描述戰鬥過程中雙方兵力隨時間的損耗關係：
式中α、β分別為藍方、紅方在單位時間內每一戰鬥單位毀傷對方戰鬥單位的數目， 簡稱為藍方、 紅方的毀傷率係數。在雙方使用步兵武器進行直瞄射擊的情況下，毀傷率係數等於武器的射速乘以單發射彈命中目標的機率與命中目標的條件下毀傷目標機率的乘積。假設交戰開始時刻藍方、紅方的初始戰鬥單位數為m(0)=M,n(0)=N，從上述微分方程組可知，在交戰過程中雙方戰鬥單位數符合下列狀態方程：
蘭徹斯特方程
蘭徹斯特方程
蘭徹斯特方程當交戰雙方的初始戰鬥單位數與毀傷率係數之間滿足時，m(t)與n(t)同時趨於零，戰鬥不分勝負。當時，藍方將首先被消滅。蘭徹斯特將上述關係概括為“在直接瞄準射擊條件下，交戰一方的有效戰鬥力，正比於其戰鬥單位數的平方與每一戰鬥單位平均戰鬥力(平均毀傷率係數)的乘積”，並稱之為“平方律”。
按照這一定律，如果藍方武器系統的單個戰鬥單位的平均效率為紅方的4倍,則紅方在數量上必須集中2倍於藍方的兵力才可抵消藍方武器在質量上的優勢。
蘭徹斯特採用下述例子說明平方律符合集中優勢兵力的作戰原則：“如果藍方1000人與紅 方1000人交戰，雙方單個戰鬥單位的平均戰鬥力相同，紅方被藍方分割成各500人的兩半。假定藍方以1000人先攻擊紅方的500人，則藍方將以損失134人的代價全殲紅方的一半，接著藍方以剩下的866人再全殲紅方的另一半，藍方在這兩次戰鬥中總共損失293人。”
直接求解上述微分方程組可以得到藍、紅雙方兵力隨時間變化的關係：
蘭徹斯特方程式中：t 表示戰鬥時刻；m(t)，n(t)表示戰鬥開始後在 t 時刻藍方、紅方在戰鬥中剩存的戰鬥單位數量；α，β 分別表示藍方、紅方在單位時間內每一戰鬥單位殺傷對方戰鬥單位的比例，即戰鬥力係數。
從這個方程中可以推導出：
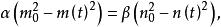蘭徹斯特方程
蘭徹斯特方程
蘭徹斯特方程即如雙方單個戰鬥單位的平均戰鬥力相等，即α=β ，上式就簡化成為 。當紅軍被全殲時，也就是 n(t)=0時，就有。
最後：
蘭徹斯特方程藍方兵力=A=1000
紅方兵力=B=B=500
作戰效率=1
藍方戰鬥力=藍方兵力×作戰效率=1000
紅方戰鬥力=紅方兵力×作戰效率=500
單位時間=1
藍方集中1000人攻擊紅方500人，則根據公式可得
第一回合
藍方剩餘兵力=√藍方戰鬥力 -紅方戰鬥力 =√750000≈866.02
第二回合
藍方剩餘兵力=√499956≈707.07
由此我們可以看出，在兩軍對壘中如果武器裝備落後於對手4倍水平級別，則必須在兵力上增派至4倍兵力數方可抵消對手在裝備上造成的壓力。即當雙方的兵力總數逼近瓶頸時，裝備的優劣是影響戰局的主要因素。
蘭徹斯特方程及其套用式中ch(·)、sh(·)為雙曲餘弦函式與雙曲正弦函式。
線性律
假定紅、藍兩軍各自使用武器(如火炮)對對方實施遠距離間接瞄準射擊，火力集中在已知對方戰鬥單位的集結地區，該區域的大小與對方部隊的數量無關。此時一方的損傷率與對方向其開火的戰鬥單位數量成正比，同時也與己方部隊在該防區內的數量成正比。這時，可用下列微分方程組來描述雙方戰鬥單位數量隨時間的變化：(t)、n(t)的含義同平方律。經簡單推導可知交戰過程中雙方兵力符合下列狀態方程：
蘭徹斯特方程
蘭徹斯特方程
蘭徹斯特方程式中M、N 的意義同平方律。交戰雙方不分勝負的條 件為，如果,則藍方將首先被消滅。蘭徹斯特將上述關係概括為“在向面目標間接瞄準射擊的條件下，交戰一方的有效戰鬥力正比於其戰鬥單位數與該方每一戰鬥單位的平均戰鬥力的乘積”，並稱之為線性律。
冷兵器時代，戰鬥形式通常是單兵之間一對一地進行格鬥，戰鬥的結局取決於雙方的格鬥水平，藍、紅雙方的平均毀傷率取常數值，分別用α、β表示，交戰過程中雙方兵力的變化可用下列微分方程組來描述：
蘭徹斯特方程式中m(t)、n(t)的含義同平方律。此時交戰過程中雙方兵力之間符合的狀態方程與向面目標進行間瞄射擊時的線性律所描述的狀態方程完全相同。這種關係可概括為“在兵一對一格鬥的條件下，交戰一方的有效戰鬥力正比於其戰鬥單位數與該方每一戰鬥單位的平均戰鬥力的乘積。”這便是描述冷兵器時代戰鬥的線性律。
為加以區別，有時將描述使用冷兵器戰鬥的線性律稱為“第一線性律”，而將描述使用火器向面目標進行間瞄射擊時的線性律稱為“第二線性律”。
擴充與推廣
現代戰鬥中所包含的各種複雜因素，遠遠超出了上述蘭徹斯特方程賴以建立的簡化了的假設條件。B.O.庫普曼等將雙方作戰單位數作為隨機變數，並運用馬爾可夫過程理論來描述交戰過程中出現的毀傷情況，從而得出隨機型蘭徹斯特方程。S.J.梯曲曼等從平方律、第二線性律的微分方程組中各取一式，以描述游擊戰中正規軍與游擊隊毀傷的情況，並由此得出“混合律”。S.邦德等研究了蘭徹斯特方程中毀傷率係數與敵對雙方的射擊狀態、武器戰術技術性能參數間的關係，從而建立了描述合成軍交戰並包含部隊增援與非戰鬥毀傷等方面的廣義蘭徹斯特方程組。H.K.威斯等將戰術決策者所採用的策略作為決策參數納入蘭徹斯特方程， 並運用最最佳化理論研究了 “最佳戰術決策”等方面的問題。J.H.恩格爾等曾運用歷史上一些著名戰鬥中雙方傷亡的數據驗證過蘭徹斯特方程的正確性。
套用
不同信息條件下的空戰效能分析
信息化條件下空戰效能，對不同信息條件下的空戰效能進行分析，建立了相對應的蘭徹斯特方程。在運用蘭徹斯特方程分析的過程中，突出了不同信息條件對空戰效能的影響，分析結果顯示了信息優勢是獲得空戰優勢的關鍵性因素，並評估了信息因素對空戰進程的決定性作用。
戰鬥機超視距空戰隱身效能分析
隨著軍事科技的進步，超視距空戰逐步成為了現代與未來空戰的主要戰鬥方式。而隱身技術作為提高戰鬥機空戰能力的主要手段之一，正被各國所關注。基於影響圖的蘭徹斯特微分方程對戰鬥機在超視距空戰中的隱身效能進行了分析，計算了不同RCS下的戰鬥機超視距空戰交換比，從而分析了戰鬥機RCS對戰場走勢的影響。
大區域防空作戰效能評估模型
針對大區域防空參戰兵力多，體系結構、交戰過程複雜的特點，引入作戰效能、戰鬥編組、火力毀傷及任務分配等矩陣，建立了基於蘭徹斯特方程的大區域防空作戰效能評估模型，包括戰鬥力指數、戰鬥編組、毀傷指數、任務分配、指揮控制和作戰實力損耗等部分。每個模型的建立均通過設定相應矩陣，分析戰鬥力指數，得出其計算模型，並以相關抗擊率以及安全率表征總體效能指標，較好地解決了對大區域防空作戰效能的評估問題。模型簡潔，便於理解，易於計算。
