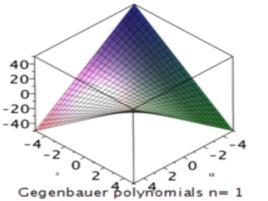
定義
記
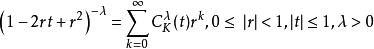蓋根堡多項式
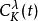蓋根堡多項式
蓋根堡多項式則係數多項式 就稱為帶參數 的k階蓋根堡多項式，也稱為超球不等式。
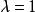蓋根堡多項式當 時蓋根堡多項式如下
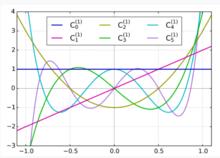蓋根堡多項式
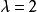蓋根堡多項式當 時蓋根堡多項式如下
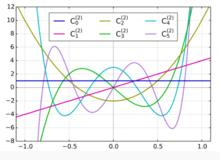蓋根堡多項式
蓋根堡多項式當是蓋根堡多項式如下：
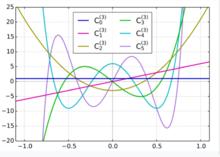蓋根堡多項式特徵
1、多項式可以根據其生成函式來定義
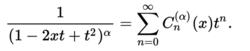蓋根堡多項式2、多項式滿足遞推關係
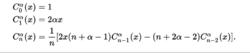蓋根堡多項式3、蓋根堡多項式是蓋根堡微分方程的特殊解
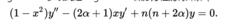蓋根堡多項式當α=1/2時，方程式減少到勒讓德方程，蓋根堡多項式減少到勒讓德多項式。
當α=0時，方程式減少到切比雪夫微分方程，蓋根堡多項式減少到第一類的切比雪夫多項式。
4、它們是雅克比多項式的特殊情況
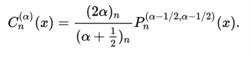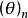蓋根堡多項式
蓋根堡多項式
蓋根堡多項式其中， 代表上升階乘的 。因此，也有羅德里格斯公式
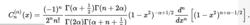蓋根堡多項式歸一化
對於一個固定的α，所述多項式是在[-1,1]相對於所述加權函式正交
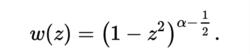蓋根堡多項式
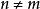蓋根堡多項式對於 而言
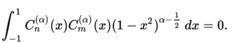蓋根堡多項式它們被歸一化
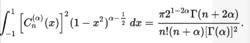蓋根堡多項式套用
在潛在理論和諧波分析的上下文中，蓋根堡多項式自然地表現為勒讓德多項式的擴展。
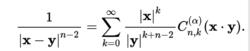蓋根堡多項式當n=3時，這給出了引力勢的勒讓德多項式擴展。類似的表達式可用於擴展球中的Poisson核心。
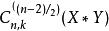蓋根堡多項式因此數量 是球面諧波，當被認為是x的函式。實際上，它們正好是帶狀球面諧波，達到歸一化常數。
蓋根堡多項式也出現在正定函式的理論中。
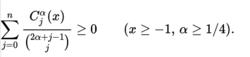蓋根堡多項式