萊莫恩定理

簡介：

萊莫恩（Lemoine）定理內容：過△ABC的三個頂點A、B、C作它的外接圓的切線，分別和BC、CA、AB所在直線交於P、Q、R，則P、Q、R三點共線。直線PQR稱為△ABC的萊莫恩線。

證明一：

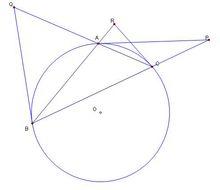萊莫恩定理

首先，由弦切角定理可以得到：

sin∠ACR=sin∠ABC

sin∠BCR=sin∠BAC

sin∠BAP=sin∠BCA

sin∠CAP=sin∠ABC

sin∠CBQ=sin∠BAC

sin∠ABQ=sin∠BCA

所以，我們可以得到：(sin∠ACR/sin∠BCR)*(sin∠BAP/sin∠CAP)*(sin∠CBQ/sin∠ABQ)=1，這是角元形式的梅涅勞斯定理，所以，由此，得到△ABC被直線PQR所截，即P、Q、R共線。

證明二

對圓內接六邊形AABBCC套用Pascal定理（其中AA邊表示過A的切線）AA∩BC=P AB∩CC=R BB∩CA=Q 所以P、Q、R共線