簡介
 范氏方程
范氏方程范德華方程( van der Waals equation)是 范德瓦耳斯方程的另一種翻譯,簡稱 范氏方程,是荷蘭物理學家范德瓦耳斯(van der Waals,又譯“范德華”、“凡德瓦耳”)於1873年 提出的一種實際氣體狀態方程。
方程形式
范德瓦耳斯方程的具體形式:
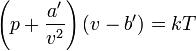 范德華方程
范德華方程式中
p為氣體的壓強
a'為度量分子間引力的唯象參數
b'為單個分子本身包含的體積
v為每個分子平均占有的空間大小(即氣體的體積除以總分子數量);
k為玻爾茲曼常數
T絕對溫度
更常用的形式為:
(p+an^2/V^2)(V-nb)=nRT
在第二個方程里
V為總體積
n為摩爾量(number of moles)
a為度量分子間引力的參數
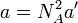 范德華方程
范德華方程b為1摩爾分子本身包含的體積之和 b= N A b',
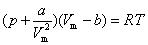 范德華方程
范德華方程R為普適氣體常數
N A為阿伏加德羅常數.
下表列出了部分氣體的 a, b的值
| 氣體種類 | a [kPa 范德華方程 范德華方程 | b [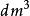 范德華方程 范德華方程 |
| 氦氣(He) | 3.45 | 0.024 |
| 氫氣(H2) | 24.32 | 0.027 |
| 氮氣(N2) | 141.86 | 0.039 |
| 氧氣(O2) | 137.80 | 0.032 |
| 二氧化碳(CO2) | 364.77 | 0.043 |
| 水蒸氣(H2O) | 557.29 | 0.031 |
在上述方程中必須嚴格區分總體平均性質和單個分子的性質。譬如,第一個方程中的 v是每個分子平均占有空間的大小(可以理解成分子平均“勢力範圍”的大小),而 b'則為單個分子本身“包含”的體積(若為單原子分子如稀有氣體, b'就是原子半徑內包含的體積)。
簡化形式
在一般形式的范氏方程中,常數a和b 因氣體/流體種類而異,但我們可以通過改變方程的形式,得到一種適用於所有氣體/流體的普適形式。
按照下面的方式定義 約減變數(亦稱 折合變數,就是把變數轉換成其 無量綱形式),其中下標R 表示約減變數,下標C 表示原變數的臨界值:
pR=p/pC,
vR=v/vC,
Tr=T/Tc
式中pC=a/27b2,vC=3b,kTc=8a/27b
用約減變數代替原變數,范氏方程形式變為
(pR+3/vR^2)(vR-1/3)=(8/3)*TR
這就是范氏方程的不變形式,即這一形式不會因套用流體種類改變而改變。
上述方程的不變性質亦稱對應態原理
適用範圍
范氏方程對氣-液臨界溫度以上流體性質的描寫優於理想氣體方程。對溫度稍低於臨界溫度的液體和低壓氣體也有較合理的描述。
但是,當描述對象處於狀態參量空間(P,V,T)中氣液相變區(即正在發生氣液轉變)時,對於固定的溫度,氣相的壓強恆為所在溫度下的飽和蒸氣壓,即不再隨體積 V(嚴格地說應該是單位質量氣體占用的體積,即比容)變化而變化,所以這種情況下范氏方程不再適用。
具體套用
在流體力學中,范氏方程可以作為可壓縮流體(如液態高分子材料)的PVT狀態方程。這種情況下,由於比容 V變化不大,可將方程簡化為:
(p+A)(V-b)=CT,
其中 p為壓強, V為比容, T為溫度, A、 B、 C均為與對象相關的參數 。

