定義
這個群包含G和H為子群,由G和H的元素生成,並且是有以上性質的群之中“最一般”的。自由積一定是無限群,除非G和H其一是平凡群。自由積的構造方法和自由群(由給定的生成元集合所能構造出的最一般的群)相似。
建構方式
若 G和 H是群,以 G和 H形成的 字是以下形式的乘積:
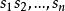 自由積
自由積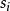 自由積
自由積其中 是 G或 H的元。這種字可以用以下的操作簡化:
•除去其中的(G或H的)單位元,
•將其中的gg一對元素以其在G中的積代替,將其中的hh一對元素以其在H中的積代替。
每個簡約字都是 G的元素和 H的元素交替的積,例如:
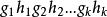 自由積
自由積自由積 G∗ H的元素是以 G和 H形成的簡約字,其上的運算是將兩字接合後簡化。
例如若 G是無窮循環群< x>, H是無窮循環群< y>,則 G∗ H的元素是 x的冪和 y的冪交替的積。此時 G∗ H同構於以 x和 y生成的自由群。
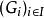 自由積
自由積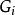 自由積
自由積設 是群的一個族。用 形成的字,也可以用上述操作簡化為簡約字。
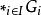 自由積
自由積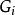 自由積
自由積仿上可定義出 的 自由積。
表示
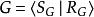 自由積
自由積設
是 G的一個展示( S是生成元的集合, R是關係元的集合)
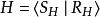 自由積
自由積又設
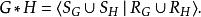 自由積
自由積是 H的一個展示。那么
即是 G∗ H是 G的生成元和 H的生成元所生成,而其關係是 G的關係元和 H的關係元所組成。(兩者都是不交並。)
性質
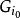 自由積
自由積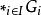 自由積
自由積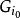 自由積
自由積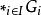 自由積
自由積將 自然地映射到 的群同態是內射,故此這個群同態將 嵌入到 中為子群。
泛性質
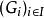 自由積
自由積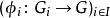 自由積
自由積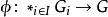 自由積
自由積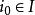 自由積
自由積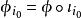 自由積
自由積設 G是群, 是由群組成的一個族,有一族群同態 。那么存在唯一的群同態 ,使得對所有 都有 。
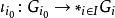 自由積
自由積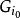 自由積
自由積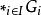 自由積
自由積其中 是把 嵌入到 中的群同態。
推廣
共合積(英語: amalgamated (free) product或 free product with amalgamation,法語: produit (libre) amalgamé)是自由積的推廣。設 G和 H是群,又設 F是另一個群,並有群同態。
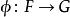 自由積
自由積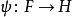 自由積
自由積及
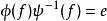 自由積
自由積對 F中所有元素 f,在自由積 G∗ H中加入關係
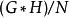 自由積
自由積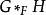 自由積
自由積便得出其共合積。換言之,在 G∗ H中取最小的正規子群 N,使得上式左方的元素都包含在內,則商群就是共合積 。
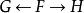 自由積
自由積共合積可視為在群範疇中圖表 的推出。
塞弗特-范坎彭定理指,兩個路徑連通的拓撲空間沿著一個路徑連通子空間接合的並,其基本群是這兩個拓撲空間的基本群的共合積。
共合積及與之相近的HNN擴張,是討論在樹上作用的群的Bass–Serre理論的基本組件。

