相關背景
自由振動
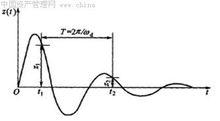
自由振動作振動的系統在外力的作用下物體離開平衡位置以後就能自行按其固有頻率振動，而不再需要外力的作用，這種不在外力的作用下的振動稱為自由振動．理想情況下的自由振動叫無阻尼自由振動．自由振動時的周期叫固有周期，自由振動時的頻率叫固有頻率．它們由振動系統自身條件所決定，與振幅無關．
自由振動與受迫振動區別：
自由振動
自由振動受迫振動也稱強迫振動．在外來周期性力的持續作用下，振動系統發生的振動稱為受迫振動．這個“外來的周期性力”叫驅動力(或強迫力)．物體的受迫振動達到穩定狀態時，其振動的頻率與驅動力頻率相同，而與物體的固有頻率無關．
而自由振動能自行按其固有頻率振動，而不再需要外力的作用
公式推導
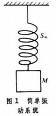
力學系統受初始擾動後，不再受其他激勵而在其平衡位置附近的振動。由於介質阻尼和內耗都看作是屬於振動系統的，因此自由振動也包括有阻尼力的振動。最簡單的自由振動就是簡諧振動。其次是有阻尼力的單自由度線性振動（見線性振動）。對於多自由度的自由振動，由於振動過程發生在系統穩定的平衡位置鄰近，若取平衡位置為廣義坐標的原點，這時系統的動能 T和勢能 V可近似地表為：
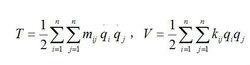自由振動式中 q為廣義坐標； m為質量； k為剛度。作用在系統上還有與阻尼力類似的耗散力。這種力學系統的運動方程為：
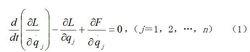自由振動，（ j=1，2，…， n） （1）
式中 F為瑞利耗散函式，； L= T－ V為拉格朗日函式。
對於保守系統， F=0，式（1）變成完整保守系統的拉格朗日方程：
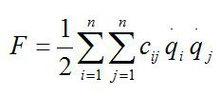自由振動。（ j=1，2，…， n）
套用上式於多自由度保守系統的自由線性振動，可得振動方程：
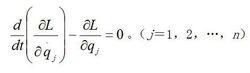自由振動， （2）
式中
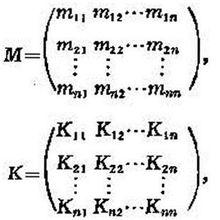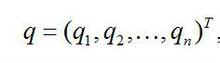自由振動
自由振動它們分別為質量矩陣、剛度矩陣和廣義位移矢量。
自由振動這種保守系統的振動特色是由各廣義位移作簡諧振動而形成的。可設主振動為： q= usin（ ωt+ ）， （3）
自由振動式中，稱為主振型矢量； q和 u都可看作列矩陣。將式（3）代入式（2）並約去sin（ωt+），得：
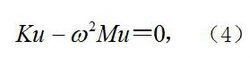自由振動上式稱為特徵矢方程，而稱為特徵矩陣。式（4）有非零解的條件為：
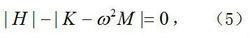自由振動式（5）稱為特徵方程；從式（5）可解出 n個（ i=1，2，…， n）。將代入式（4）後，可解得對應於的 n個。稱固有頻率（主頻率），或特徵值；稱固有振型（主振型）或特徵矢量。當 K和 M為 n階實對稱矩陣，且 M正定時，存在 n個實特徵值和相應的 n個特徵矢量，故式（2）的特解可寫為：
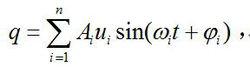自由振動式中和是待定常數，由初始條件決定。例如已知 t=0時的和，則有：
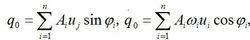自由振動從而可求出和（ i=1，2，…， n）。
