彈性體的線性振動
正文
彈性體受到的激勵和由此引起的回響呈線性關係的振動。可以用線性方程描述。實際結構的各種小振動都可看作彈性體的線性振動,例如,鋼琴中被張緊的弦的振動,帶汽缸、螺旋槳的軸系旋轉時的扭轉振動,鑽桿的縱振動以及各種複雜結構的地震回響。當彈性體在穩定平衡位置附近振動,而振幅又是夠小時,彈性體的應力-應變(見應力和應變)關係、應變-位移關係都可以近似當作線性的。因此,所有外界激勵因素引起的振動回響是各個激勵因素分別引起的回響的疊加,而且回響和激勵成正比。
研究彈性體的線性振動一般是研究其固有振動、自由振動和受迫振動。
固有振動 在一定的初始條件下,彈性體將產生一類特殊的振動,其特點是:物體的每點都作同頻率、同相位的簡諧振動,而各點的振幅保持一定的比例,這種振動稱為固有振動,其頻率稱為固有頻率,各點振幅構成的形狀稱為固有振型或主振型,簡稱振型。彈性體有無窮個固有振動,有限尺寸的彈性體的固有頻率是離散的,若將這些固有頻率的數值按升序排列,數列趨於無窮,其中最小的固有頻率稱為基頻。對某些彈性體,有的固有頻率對應幾個線性獨立的振型,但其個數必然是有限的。對應不同固有頻率的振型存在著以質量為權函式的正交關係,它表示振型之間沒有能量交換。
自由振動和受迫振動 彈性體受到初干擾就作自由振動。在實際結構中,自由振動會因阻尼作用而逐漸衰減。若彈性體的初位移和初速度和某一固有振型成正比,則自由振動就是相應的固有振動。
由隨時間變化的外力或給定的某些部分的隨時間變化的位移引起的振動為受迫振動。若外力隨時間作簡諧變化,而且變化頻率和彈性體的某一固有頻率接近,則在一般情況下,振幅會急劇增大,這種現象稱為共振。此時彈性體振動的形狀近似於相應的振型。共振頻率有無窮多個,但由於阻尼的存在,實際上只有在外力的頻率和比較低階的固有頻率接近時才可能產生共振。
彈性體的自由振動和受迫振動都稱為彈性體的回響。它們不僅取決於初干擾和外激勵,而且取決於固有頻率和振型。研究彈性體的回響,可將它們展成固有振型的級數,其係數是時間的函式,它們取決於初干擾、外激勵的形式以及激勵頻率和固有頻率的關係。利用振型的正交性可確定這些係數,從而得到彈性體的回響。這就是(固有)振型疊加法。因此,在彈性體的振動分析中,無論避免共振,利用共振的性質,還是確定動態回響,首要的任務是找出固有頻率和振型,其方法很多,有理論方法(見計算結構力學),也有實驗方法(見振動試驗)。
常見彈性體的固有振動
①弦的振動 兩端固定的張緊的弦作固有振動時,固有頻率為:
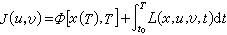
兩端固定的張緊弦的固有振型是一族正弦曲線,取一弦端為x軸原點,則對應第n階固有頻率fn的振型為:
φn(x)=Asin(nπx/l),
式中A為最大振幅。 圖1表示出兩端固定的弦的1、2、3階振型。 對應不同頻率的振型之間的正交關係為: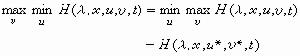 。
。
②梁的振動 矩形截面梁作橫向振動的振型由正弦、餘弦、雙曲正弦和雙曲餘弦函式線性組合而成,其固有頻率為:

。
圖3表示出一些方膜的振型。方形膜上位移為零的線稱為節線(圖中用虛線表示),φ1,2和φ2,1的節線分別是y=l/2和x=l/2。由於φ1,2和φ2,1對應同一固有頻率,所以根據線性振動的可疊加性,它們的任意線性組合也是這一固有頻率的振型(圖3之c、之d、之e)。高階的振型會出現更複雜的圖型。