定義
 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點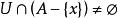 完全聚點
完全聚點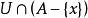 完全聚點
完全聚點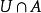 完全聚點
完全聚點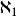 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點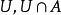 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點若為的聚點,則對於的任意鄰域,有,還可根據的基數而將聚點分類。當的基數是以上時,稱為的 凝聚點(condensationpoint),當對所有的鄰域的基數都等於的基數時,稱為的 完全聚點或 最大聚 點 。
相關概念
 完全聚點
完全聚點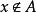 完全聚點
完全聚點 完全聚點
完全聚點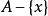 完全聚點
完全聚點 完全聚點
完全聚點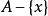 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點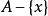 完全聚點
完全聚點 完全聚點
完全聚點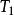 完全聚點
完全聚點 完全聚點
完全聚點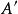 完全聚點
完全聚點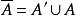 完全聚點
完全聚點 完全聚點
完全聚點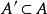 完全聚點
完全聚點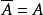 完全聚點
完全聚點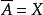 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點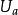 完全聚點
完全聚點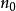 完全聚點
完全聚點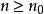 完全聚點
完全聚點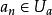 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點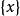 完全聚點
完全聚點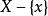 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點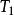 完全聚點
完全聚點定義1 聚點為子集A的 聚點(可能),是指的任一開鄰域含的點,等價於含於的閉包(當第1可數時,等價於是中點列的極限點;進而為第1可數且時(如度量拓撲),等價於為A的互異點構成的點列的極限)。聚點集稱 導集。非聚點稱為 孤立點。,即閉包=導集U原集(觸點=聚點和原集點)。A為閉集(即)。A的閉包的余集稱為A的外部(即非觸點集),閉包與余集閉包之交為邊界。若閉包則稱A在X中 稠密。點列收斂於(稱為 極限)是指:對於的任一鄰域,存在,使當時。點稱為A的 完全(最大)聚點,是指的任一鄰域U與A的交的基數等於A的基數。一點為閉集( 一點閉集)若且唯若中任一點有開鄰域不含。X中任一點為閉集相當於X為。
 完全聚點
完全聚點 完全聚點
完全聚點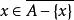 完全聚點
完全聚點 完全聚點
完全聚點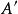 完全聚點
完全聚點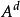 完全聚點
完全聚點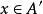 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點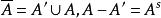 完全聚點
完全聚點 完全聚點
完全聚點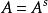 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點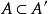 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點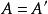 完全聚點
完全聚點 完全聚點
完全聚點定義2 設為的一點,A為X的子集,若,則稱為A的 聚點(英accumulation point)。A的聚點集稱為A的 導集(derived set),以或表示之。與的任意鄰域最少含有以外的的一個點,二者是等價的。的點稱為的 孤立點(isolated point),僅由孤立點組成的集合(時)稱為 孤點集(isolated set)或 離散集(discrete set)。當的任意非空子集都具有孤立點時稱為 無核集(scattered set)。當不具有孤立點時(時),稱為 自密集(dense in itself)。的自密的子集中最大者稱為的 自密核(德insichdichterKern)。當時稱為 完備集(perfect set) 。
 完全聚點
完全聚點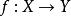 完全聚點
完全聚點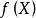 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點 完全聚點
完全聚點緊緻性 這是中有界集的推廣。若拓撲空間X的任意開覆蓋有有限子覆蓋,則稱X為 緊(致)的。等價於以下每一條:(1)若一閉集族的任意有限子族有交,則全族有交;(2)無限子集總有完全聚點;(3)有向點族總有收斂子族(點族有向是指:點族有半序,且其有限子集上方有界(不一定屬於此子集))。子集A是 緊子集是指作為子拓撲空間A是緊的(相當於A的“開集屬於X的開覆蓋”總有有限子覆蓋)。緊拓撲空間的閉子集是緊的。Hausdorff空間中緊子集是閉的。故緊Hausdorff空間正規。緊X上的連續映射的象緊;再若為Hausdorff,則為閉映射;再若為雙射,則為同胚。直積空間是緊的若且唯若各分空間是緊的。緊Hausdorff空間是正規的,可賦予距離等價於第2可數。離散空間中僅有限集是緊的。非緊的X可增點而“一點緊化”:開集為原開集,以及含的子集而余集在X中緊閉者 。

