基本介紹
前提格
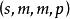 結論格
結論格量化擴展的三段論的前提的4個項 的分布位置的不同排列稱為擴展的三段論的 前提格。擴展的三段論的前提格分為4個格,參見表1 。
| 前提第1格 | 前提第2格 | 前提第3格 | 前提第4格 | |
| 前提1 | 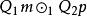 結論格 結論格 | 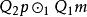 結論格 結論格 | 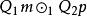 結論格 結論格 | 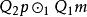 結論格 結論格 |
| 前提2 | 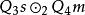 結論格 結論格 | 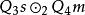 結論格 結論格 | 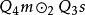 結論格 結論格 | 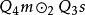 結論格 結論格 |
| 結論第1格 | 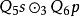 結論格 結論格 | 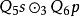 結論格 結論格 | 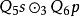 結論格 結論格 | 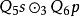 結論格 結論格 |
| 結論第2格 | 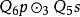 結論格 結論格 | 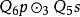 結論格 結論格 | 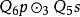 結論格 結論格 | 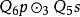 結論格 結論格 |
例1:前提第3格的式(包括式的相關概念命名規則說明):
在表1中,由於每個量詞均有3種(即1,2,3,亦即〒,∀,∃)選擇,那么
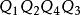 結論格
結論格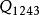 結論格
結論格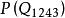 結論格
結論格前提第3格的量詞序列是 的不同取值 的排列 ,即:
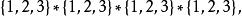 結論格
結論格 結論格
結論格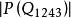 結論格
結論格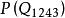 結論格
結論格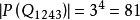 結論格
結論格其中 表示笛卡兒積。以 表示 方案的數量,則 。
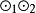 結論格
結論格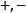 結論格
結論格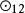 結論格
結論格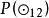 結論格
結論格前提第3格的系詞序列為 ,每個系詞均有2種(即 )選擇,那么前提第3格的系詞序列是變數值不同取值 的排列 ,為
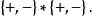 結論格
結論格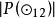 結論格
結論格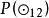 結論格
結論格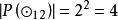 結論格
結論格以 表示 方案的數量,則 。
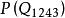 結論格
結論格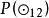 結論格
結論格以mood | H-figure3表示前提第3格的式,那么,前提第3格的式mood | Hfigure3是 和 的組合,即
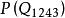 結論格
結論格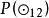 結論格
結論格mood | H-figure3= ×
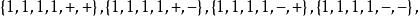 結論格
結論格={
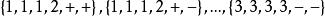 結論格
結論格}.
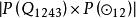 結論格
結論格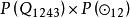 結論格
結論格以 表示 方案的數量,那么前提第3格的前提式的總數為
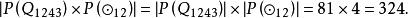 結論格
結論格同樣,其他3個前提格的式的總數也分別為324。
結論格
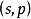 結論格
結論格量化擴展的三段論的結論的2個項 前後分布的位置的不同排列構成擴展的三段論的 結論格。擴展的三段論的結論格分為2個格,參見表1。
一個擴展的三段論舉例如下:部分m是部分p,並且所有s不是m,存在p不是s 。
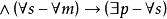 結論格
結論格其符號表示為(〒m〒p) 。
按與例1命名法則相同的命名規則,相應地命名mood | C-figure1=P(Q)×P(⊙)為結論第1格的式。那么,結論第1格的式的總數為
|P(Q)×P(⊙)|=|P(Q)|×|P(⊙)|=3×3×2=18
同樣,結論第2格的式的總數也為18。
擴展的三段論的格式
對擴展的三段論的格式系指擴展的三段論的前提格與前提式進行排列,結論格與結論式進行排列,則這兩個排列的排列是擴展的三段論的格式 。
總之,擴展的三段論的格式是量詞和系詞的不同取值以及在前提和結論中s和p的不同位置的所有不同方案。
擴展的三段論的前提格與前提式的組合方案是:
mood | H-figure1~4
={P(Q),P(Q),P(Q),P(Q)}×{P(⊙)}
其方案總數是:
|{P(Q),P(Q),P(Q),P(Q)}×{P(⊙)}|=81×4×4=1296
擴展的三段論的結論格與結論式的組合方案是:
mood | C-figure1~2={P(Q),P(Q)}×{P(⊙)}
其方案總數是:
|{P(Q),P(Q)}×{P(⊙)}|=3×2+3×2=36
相關概念
量化擴展的直言原子命題
定義1量化擴展的直言原子命題是如下結構的直言命題,但是否定謂詞後面禁止跟有部分量詞和存在量詞:
 結論格
結論格其中:
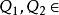 結論格
結論格 結論格
結論格{〒, };
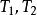 結論格
結論格是項;
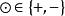 結論格
結論格,+和一分別表示“是”和“不是”,“+”可省略。
量化擴展的直言命題形式是完善的,其完善性表現在量詞樣本的完全性:
 結論格
結論格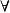 結論格
結論格(1)量詞是確定和不確定的樣本的集合,它是判斷過程所有可能的兩種狀態;不確定量詞即存在量詞 ;確定量詞包括全稱量詞 和部分量詞〒。因此,量化擴展的直言命題的量詞體系包括了數量的離散狀態中關於確定性的所有兩種可能的狀態,以及確定性狀態中是否是全集的所有兩種可能的狀態。
(2)除否定系詞後面沒有部分量詞和存在量詞外,這些命題形式是關於三個量詞在兩個項的約束位置的全排列,即擴展的直言命題形式是在約束條件(否定系詞後面禁止部分量詞和存在量詞)下關於量詞在前後位置排列的所有樣本的集合。這些樣本即〒〒,〒∀,∀〒,∀∀,∀∃,∃∀,∃∃,〒∃,∃〒。
由於上述兩點改進,直言命題消除了不一致性(不相容性)以及後項沒有約束量詞造成的邏輯歧義。
量化擴展的三段論
考慮用三個量化擴展的直言命題構成的新的三段論——量化擴展的三段論。
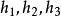 結論格
結論格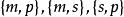 結論格
結論格定義1對於任意3個量化擴展的直言命題 ,如果它們的二元項分別是 ,則下列命題稱為 量化擴展的三段論:
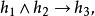 結論格
結論格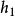 結論格
結論格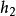 結論格
結論格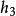 結論格
結論格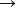 結論格
結論格其中: 和 分別為前提1和前提2; 為結論; 表示蘊涵。
直言三段論
直言三段論是由直言命題所組成的一種推理形式,簡稱三段論。傳統邏輯的三段論演繹體系是由亞里士多德創立的,在中世紀得以完善,現代的數理邏輯對三段論也作過專門的研究。
三段論的結構
一個直言三段論由三個直言命題所組成,其中兩個為前提,一個為結論。三個直言命題包含三個不相同的詞項,其中只在兩個前提中出現而不在結論中出現的詞項稱為中項,用字母“M”表示;在結論中作為主詞的詞項稱為小項,用字母“S”表示;在結論中作為賓詞的詞項稱為大項,用字母“P”表示。兩個前提中包含大項的前提稱為大前提,包含小項的前提稱為小前提。在排列順序上,通常大前提在前,其後是小前提,最後為結論。但這種順序不是絕對的。
三段論的公理
又稱曲全公理。直言三段論推理的依據。內容為:凡對一類事物有所肯定,則對該類事物中的每一個對象也有所肯定;凡對一類事物有所否定,則對該類事物中的每一個對象也有所否定。三段論的規則
要保證直言三優論推理的有效性,就必須遵守一定的規則。三段論的規則共二類四條。第一類是關於詞項的規則:(一)在前提中,中項至少要周延一次;(二)詞項只有在前提中周延,才可在結論中周延。第二類是關於質的規則:(一)至少有一個前提必須是肯定的;(二)如果有一個前提是否定的,則結論必須是否定的。以這四條基本規則也可以證明一些從屬的規則,例如,兩個特稱的前提推不出結論;如果前提中有一個是特稱的,則結論必須是特稱的;如果結論是肯定的,則兩個前提必須是肯定的;如果結論是全稱的,則兩個前提必須是全稱的;如果結論是否定的,則兩個前提中必須有一個是否定的。
三段論的格
直言三段論中由於中項在前提中的位置不同而構成的不同形式。三段論有四個格。第一格,中項是大前提的主詞,小前提的賓詞。第二格,中項在大小前提中都是賓詞。第三格,中項在大小前提中都是主詞。第四格,中項是大前提的賓詞,小前提的主詞。四個格的結構如下圖:
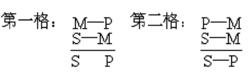 圖1
圖1 圖2
圖2根據三段論總的規則,結合各個格具體形式,可以引申出每格的具體規則。第一格:(一)大前提須是全稱的;(二)小前提須是肯定的。第二格:(一)兩個前提中須有一個是否定的;(二)大前提須是全稱的。第三格:(一)小前提須是肯定的;(二)結論須是特稱的。第四格:(一)如果大前提是肯定的,則小前提必須是全稱的;(二)如果小前提是肯定的,則結論必須是特稱的;(三)如果前提中有一個是否定的,則大前提必須是全稱的。
三段論的式
直言三段論的大前提、小前提和結論都可能由A、E、I、O中任一個命題充當,共有64種可能的組合;再考慮三段論有四個格,就有256種可能的組合每一種組合稱為一個式。在256個式中,符合三段論規則的叫有效式,違反三段論規則的叫無效式。三段論的有效式共24個,分別如下:
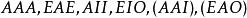 結論格
結論格第一格: ;
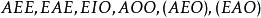 結論格
結論格第二格: ;
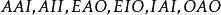 結論格
結論格第三格: ;
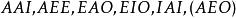 結論格
結論格第四格: 。
上例各式中19個不帶括弧的叫強式,5個帶括弧的叫弱式。弱式本可以得出全稱命題為結論,但只以特稱命題為結論。中世紀經院邏輯為了便於記憶,分別給這19個強式以特殊的名稱。並編成“格式歌訣”。例如,Barbara,Celarent分別表示第一格的AAA式和EAE式。除了這24個有效式外,其餘的232個式是無效式。
三段論的化歸
在傳統邏輯中,直言三段論是一個近似完整的公理體系。其中,第一格的AAA式和EAE式起著分理的作用,其他17個強式的有效性須通過這兩個式加以證明。證明的方法是用有效的邏輯方法把這17個式化歸(又叫還原)為第一格的AAA式和EAE式。化歸方法有兩種。一種是直接化歸,將前提或結論換位,或將兩前提對調,就可把其他格化歸為第一格。例如,第三格的IAI式具有下面的形式:
MIP
MAS/SIP
把它的大前提換位,再把大小前提對調,最後把結論換位,即成為:
MAS
PIM/PIS
這就是第一格的形式。另一種是間接化歸,使用歸謬法,把否定了的結論與一個否定了的前提對調,從而化歸為第一格。例如,第二格的AOO式具有下面的形式:
PAM
SOM/SOP
把結論SOP否定,得SAP;再把前提中的SOM否定,得SAM;然後把它們對調、即成為
PAM
SAP/SAM
這就是第一格的AAA式,所以使用這種方法,是因為前提中含有0命題,而0命題是不能換位的。
三段論的現代研究成果
用謂詞邏輯的符號來表示三段論的推理式,則三段論的有效式都可從謂詞邏輯系統中推出,其中9個從兩個全稱前提得出特稱結論的式,須將主詞存在這一傳統邏輯隱含的前提揭示出來。這表明三段論推理只是謂詞邏輯的一部分。盧卡西維茨(1878—1965)用數理邏輯為工具,對三段論體系作了專門研究。他用a、b、c等表示項詞,用△,I代表運算元,採用前置號的方法,Aab表示所有a是b,Iab表示有的a是b。將Eab(所有a不是b)定義為Iab的否定,Oab(有的a不是b)定義為Aab的否定。用下面4條公理:
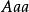 結論格
結論格(一)
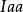 結論格
結論格(二)
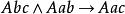 結論格
結論格(三)
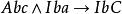 結論格
結論格(四)
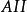 結論格
結論格其中第三條公理是三段論第一格的AAA式,第四條公理是第三格的 式。再藉助代入規則、分離規則以及命題演算的規律,就可推出直言命題的換位規律和所有的三段論的有效式。這個完全形式化的三段論公理系統的建立使人們對傳統邏輯的三段論體系有了新的認識 。

