概念
在計算機中表示一個數值型數據,要考慮如下3個問題。
確定數的長度
在數學中,數的長度是指它用十進制表示時所占用的實際位數,如9632的長度為4。在計算機中,數的長度按“比特”(bit)來計算。bit是英文binary digit(二進制位)的縮寫。但因存儲容量常以“位元組”(byte。等於8bit)為計量單位,所以數據長度也常以位元組為單位計算。值得指出的是,數學中的數的長度有長有短,如l35的長度為3,9632的長度為4,有幾位就寫幾位。但在計算機中,同類型的數據(如同屬整型數的兩個數據)的長度常常是統一的,不足的部分用“0”填充。這樣便於統一處理。換句話說,計算機中同一類型的數據具有相同的數據長度,與數據的實際長度無關。
確定數的符號
由於數據有正負之分,在計算機中必然要採用一種方法來描述數的符號。一般總是用數的最高位(左邊第一位)來表示數的正負號,並約定以“0”表示正,以“1”表示負。
小數點的表示方法
在計算機中表示數值型數據,其小數點的位置總是隱含的,即約定小數點的位置,這樣可以節省存儲空間。
定點數表示
在定點數的表示方法中,小數點的位置一旦約定,就不再改變。常用的定點數表示方法有以下兩種。
定點整數
即小數點的位置約定在最低數值位的後面,用於表示整數。例如,假設計算機使用的定點數的長度為兩個位元組(即16位二進制數),則(一193)10在機內的表示形式如下:
1000000011000001;
注意到(193)10=(11000001)2,由於11000001不足15位,故前面補足7個0,最高位用1表示負數。
定點小數
即小數點的位置約定在數符位和數值部分的最高位之間,用以表示<l的純小數。例如,假定定點數的長度仍為兩個位元組,則(0.6876)10在機內用定點數表示的形式如下:
0101100000000011;
實際上,(0.6876)10=(0.10110000000001101…)2,由於最高位用以表示符號,故兩個位元組可以精確到小數點後第15位。
浮點數表示
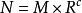 純二進制數
純二進制數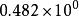 純二進制數
純二進制數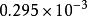 純二進制數
純二進制數浮點數的思想來源於數學中的指數表示形式:。例如:(256)10可以表示為0.256x10³;(0.482)10可以表示為;(0.000295)可以表示為。
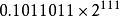 純二進制數
純二進制數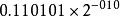 純二進制數
純二進制數類似地,二進制數(1011011)2可以表示;(0.00110101)2可以表示為。
浮點表示法中的尾數與階碼
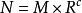 純二進制數
純二進制數對於一個R進制數,只要唯一確定M與c的值(|M|<1),則該數的值就唯一確定了,即的值就唯一確定了。因此,在計算機中,對於一個二進制的浮點數(R=2),只需要存儲M與G的值就可以了。M與C分別稱為尾數與階碼。
1)尾數M(Mantissa)。尾數為<l的純小數,表示方法與定點數中的純小數表示方法相似,其長度將影響數的精度,其符號將決定數的符號。
2)階碼C(Characteristic)。階碼相當於數學中的指數,它應當是一個整數,其表示方法與定點數表示一個整數的方法類似。
浮點數的表示形式
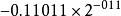 純二進制數
純二進制數假定一個浮點數用4個位元組來表示,則一般階碼占用一個位元組,尾數占用3個位元組,且每部分的最高位均用以表示該部分的正負號。例如,在機內的表示形式如下:
10000011111011000000000000000000;
值得一提的是,即使用4個位元組來表示一個定點數,4個位元組表示的浮點數的精度和表示範圍都遠遠大於定點數,這是浮點數的優越之處。但在運算規則上,定點數比浮點數簡單,易於實現。因此,一般計算機中同時具有這兩種表示方法,視具體情況進行選擇套用。

