定義
用一位二進制位表示數的符號：0表示正數，1表示負數，這種表示數的方法，稱為帶符號數的表示方法。所表示的數，叫做帶符號的數。帶符號的數其最高位為符號位。
如果將全部有效位都用來表示數的大小，這種數的表示方法，叫無符號數的表示方法，所表示的數，叫無符號數。
真值與機器數
真值就是利用"+"、"-"表示數的符號，數值部分為數的絕對值。例如：N1=+1101001B= +105；N2=-1101001B=-105。數的真值可以使用二進制形式、八進制形式、十進制形式或十六進制形式表示。
機器數就是在機器中用最高位表示數的符號，其它位表示數值的大小。這時最高位叫做符號位，規定用“0"表示正，“1’’表示負。這樣對於n位二進制數，如果它是一個帶符號的數，則最高位Bn-1就表示數的符號，剩下的n-1位表示數的大小。簡單的說，機器數就是數據在機器中的二進制表示形式，機器數所表示的值稱為該機器數的“真值”。
例如：一個帶符號的數11101001B，最高位"1"為符號位，代表“-”其它位為數的值，它的真值為：-1101001B(-105)。
X進制數
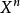數表示法對於任意一個數(十進制數)都可以表示成按權(n為整數)展開的多項式，這裡X稱為基數。對於不同的X，形成相應的X進制數。X進制數隻包含數字元號0,1，...，X-1，並且在運算過程中“逢X進一，借一當X”。常用的X進制數有二進制數、八進制數、十進制數和十六進制數。其中，十六進制包含數字元號0，1，...，9，A，B，C，D，E，F。
例如，對於數210分別用二進制、八進制、十進制、十六進制表示如下：
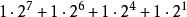數表示法二進制：210==11010010(B)；
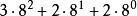數表示法八進制：210==322(O)
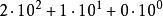數表示法十進制：210==210(D)
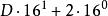數表示法十六進制：210==D2(H)
機器數表示法
機器數在計算機中的表示方法有三種，即原碼、反碼和補碼，最常用的是原碼和補碼兩種，原碼錶示法比較直觀，補碼運算則比較簡單。
原碼
原碼錶示法是一種直觀的機器數表示法，用最高位表示符號，符號位為0表示該數為正，符號位為1表示該數為負，有效數值部分用二進制絕對值表示。如真值為+0.1010和-1100其原碼為0.1010和11100。用原碼作乘除法時，可取其絕對值(尾數)直接運算，再按同號相乘除為正，異號相乘除結果為負的原則單獨處理符號，但對常用的加減法運算，卻極不方便，由此引進補碼的概念。
補碼
補碼是讓數的符號位也作為數的一部分參與運算，使實際操作僅與指令規定的操作性質有關，而與數的符號無關。即確定一個數作模以後，將某數X對模M的補數稱為X的補碼，表示為[X]補=M+X (Mod M)，正數的補碼與原碼一樣，但是捨去了模。如x=0.101，[x]補=0.101 (mod 2)，對於負數，補碼的尾數與原碼不同，其符號位在形式上與原碼相同，也用1表示負數，但這個1是通過模獲得的，也是數值的一部分，可與尾數一起參與運算，如x=-0.101，則[x]補=2+(-0.101)=1.011 (mod 2)。
對補碼的求值，一般是通過原碼轉化而來。對正數，[x]原=[x]補；對負數，符號位保持不變，尾數各位變反，然後末位加1，即“變反加1”。如：[x]原=1.1010，則[x]補=1.0110。
反碼
反碼錶示法僅對尾數逐位取反而不在末位加1，它可以達到化減為加的目的。正數反碼與原碼、補碼相同，負數反碼的符號位為1，其尾數可由其絕對質逐位反而得，符號位也參與計算。具體表示為：x=0.101，x反=0.101；x=-0.101，x反=1.010。
小數表示方法
計算機中，小數點的表示有兩種方法，即定點和浮點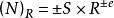表示法。
數表示法對於數，其中，N代表數字，S代表尾數，R代表基數，e代表階碼，即小數點的實際位置。
定點表示法
定點表示法中，e的取值固定不變。定點表示法中有下述兩種方法：
(1) 純小數表示法：數符·尾數；
(2) 整數表示法：數符 尾數。
定點表示法具有如下缺點：
(1) 表示的數據範圍小；
(2) 使用不方便，運算精度低，浪費存儲單元。
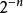數表示法定點數的解析度為：在字長為n+1的計算機中。純小數的解析度為，純整數的解析度為1。
浮點表示法
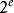數表示法
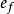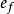數表示法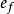 數表示法 數表示法浮點表示法中，小數點的位置是不定的，可以浮動。一個二進制數可表示為：N=·S，其中S為數N的尾數，表示數N的有效值，用S表示尾數的符號，S=0為正數，S=1為負數；e為數N的階碼，表示小數點的位置，用表示階碼的符號，=0為正數，=1為負數。
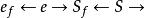數表示法具體用二進制數表示為：。
浮點數數據範圍：
(1) 最大正數和最小正數的區間，稱為正數區；
(2)最小負數和最大負數的區間，稱為負數區；
(3)最大負數和最小正數之間的區域，由於絕對值小於可表示的值。所以稱為下溢區，一般用0表示。稱為機器零。
(4)處於最大正數和最小負數之外的區間，稱為上溢區。最大正數以外稱為正溢區，最小負數以外稱為負溢區。
