基本介紹
簡單n線形n條直線(其中無三線共點)及其兩兩順次相交的交點所構成的圖形,這n條直線稱為邊,n個交點稱為頂點。
簡單n點形n個點(其中無三點共線)及其兩兩順次連線所構成的圖形,這n個點稱為頂點,n條直線稱為邊。
對於簡單n點(線)形,表1和表2分別給出了n=3和n=4的情形,顯然,對於給定的n個點(或n條直線),由它們所構成的簡單n點形(簡單n線形)與這n個點(n條直線)的排序有關。此外,這兩類圖形與初等幾何中的多邊形也是不同的概念 。
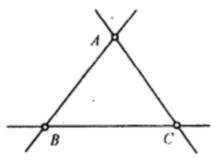 簡單n線形 簡單n線形 | 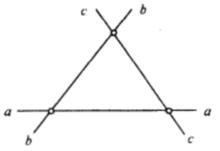 簡單n線形 簡單n線形 |
 簡單n線形 簡單n線形 | 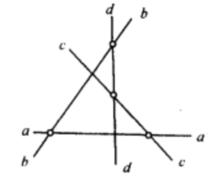 簡單n線形 簡單n線形 |
相關概念
完全n點形和完全n線形
完全n點形 n個點(其中無三點共線)及其每二點連線所構成的圖形,不難看出,完全n點形共有n個頂點,n(n- 1)/2條邊 。完全n線形 n條直線(其中無三線共點)及其每二條直線的交點所構成的圖形。不難看出,完全n線形共有n條邊,n(n-1)/2個頂點。
 簡單n線形 簡單n線形 | 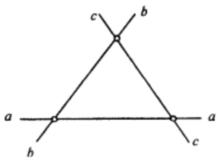 簡單n線形 簡單n線形 |
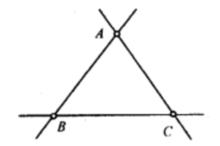
注意, 完全形與初等幾何中的n邊形沒有任何共同之處,對於給定的n個點(其中無三點共線)或n條線(其中無三線共點),由其決定的完全n點形或完全n線形是惟一的 。最常見的例子是n=3,三點形與三線形(如表3),這是一對 自對偶圖形。最重要的例子是完全四點形與完全四線形,因為這一對圖形中蘊含著十分重要的射影性質,其套用將在今後無可避免地反覆出現,一定要熟練地掌握這一對對偶圖形 。
| 名稱 | 完全四點形ABCD | 名稱 | 完全四線形abcd |
| 頂點 | A,B,C,D (4個) | 頂點 | P,Q; R,S; T,U axc,bxd;axb,cxd;axd,bxc(6個) |
| 邊 | p,q;r,s;t,u AC,BD;AB,CD;AD,BC(6條) | 邊 | a,b,c,d (4條) |
| 對邊 | 沒有公共頂點的邊 p,q;r,s;t,u (3組) | 對頂 | 不在同一條邊上的頂點。 P,Q; R,S; T,U (三組) |
| 對邊點 | 對邊的交點 X, Y, Z pxq; rxs; txu (3個) | 對頂線 | 對頂的連線 x, y, z PQ; RS; TU (3條) |
| 對邊三點形 | 三點形XYZ | 對頂三角形 | 三線形xyz |
簡單四線形和簡單四點形
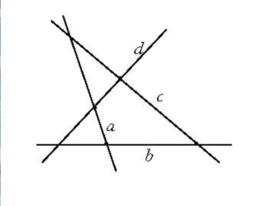
由四條直線(其中無三者共點)a,b,c,d及它們順次兩兩交點(a,b),(b,c),(c,d)、(d,a)所組成的平面形叫做簡單四線形。a,b,c,d叫做邊,(a,b),(b,c),(c,d),(d,a)叫做頂點,不順次兩邊的交點(a,c),(b,d)叫做對邊點(圖1) 。
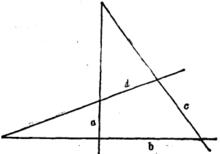 圖1
圖1簡單四點形 由四個點(其中無三者共線)A,B,C,D及它們順次兩兩的連線AB,BC,CD,DA所組成的平面形叫做簡單四點形。A,B,C,D叫做頂點。AB,BC,CD,DA叫做邊,不順次的頂點的連線AC,BD做對頂線(圖2)。
注意:簡單四點形的構成與頂點的順序有關,如圖2表示四點形ABCD,它與四點形ACBD,BDAC等不同,同樣,簡單四線形的構成與邊的順序有關 。
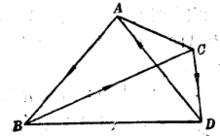 圖2
圖2