定義
設G=(V,E)是圖,若G中既無吊環又無多重邊,則稱G是簡單圖(simplegraph),如下圖,圖1是簡單圖,圖2是彼得森(Petersen,1831—1910)圖,它是一個有著特殊性質的簡單圖,一種妖怪圖(snark graph)。
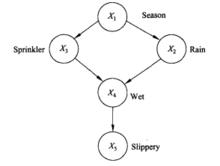 圖1
圖1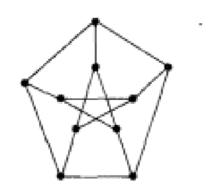 圖2
圖2幾種簡單圖舉例
完全無向圖
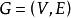 簡單圖
簡單圖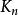 簡單圖
簡單圖設 是n階簡單無向圖,若G中任意節點都與其餘n一1個節點鄰接,則稱G為n階完全無向圖(Complete Graph),記為 。
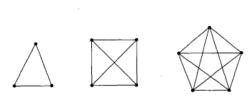 圖3
圖3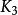 簡單圖
簡單圖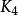 簡單圖
簡單圖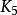 簡單圖
簡單圖圖3所示分別是、 和。
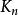 簡單圖
簡單圖將n階完全無向圖 的邊任意加一個方向所得到的有向圖稱為n階 競賽圖。
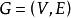 簡單圖
簡單圖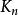 簡單圖
簡單圖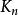 簡單圖
簡單圖設 是n階簡單有向圖,若G中任意節點都與其餘n-1個節點鄰接,則稱G為n階 完全有向圖。顯然,n階完全有向圖 的任意兩個節點都是相互鄰接的,其邊是成對出現的。容易證明,n階完全無向圖 的邊數為
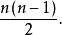 簡單圖
簡單圖補圖
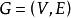 簡單圖
簡單圖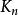 簡單圖
簡單圖 簡單圖
簡單圖設 是n階簡單無向圖,由G的所有節點以及由能使G成為 需要添加的邊構成的圖稱為G的 補圖,記為 。
如圖4所示的圖互為補圖,它們是相對於完全圖而言的。
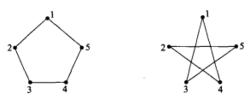 圖4
圖4 簡單圖
簡單圖 簡單圖
簡單圖顯然,對於任意節點u和v,若u和v在G中不鄰接,則u和v在 中鄰接,若u和v在G中鄰接,則u和v在 中不鄰接。
相關知識點
圖G(graph)主要由如下兩部分組成。
(1)節點集合V,其中的元素v稱為 節點(vertex或node);
(2)邊集合E,其中的元素稱為 邊(edge)。
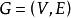 簡單圖
簡單圖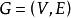 簡單圖
簡單圖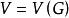 簡單圖
簡單圖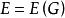 簡單圖
簡單圖通常將圖G記為 ,一個圖是一個集合上的一種二元關係,這個集合的元素稱為圖的節點,若兩節點之間有這種確定的二元關係,則稱有一條邊連這兩個節點,一個圖的節點的數目稱為這個圖的 階;圖的邊的數目稱為它的度。在文獻中,總是將一般的圖記為 ,其中, 和 分別表示G的節點集和邊集。
需要說明的是:
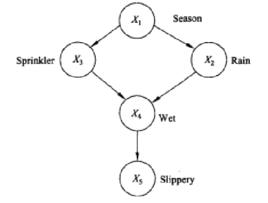
①節點又可以稱為點、頂點或結點,常用一個實心點或空心點表示,但在實際套用中還可以用諸如方形、圓形、菱形等符號,為了方便可以在這些符號的旁邊或內部寫上表意名稱,如圖5所示是一個典型的貝葉斯網路(Bayesian networks)。
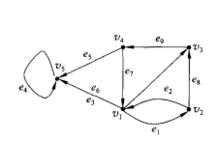 圖5
圖5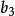 簡單圖
簡單圖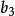 簡單圖
簡單圖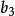 簡單圖
簡單圖②邊及其的表示.在圖6中的邊如 是沒有方向的,稱為無向邊,可以認為A是起點B是終點,也可以認為B是起點A是終點,這時A和B稱為邊 的端點(endvertices),在不致混淆時可將邊 ,簡記為AB、BA、{A,B}或{B,A},表示邊的集合{A,B}={B,A}中的兩元素可以相同,是可重集合,與通常的集合有所不同.有方向的邊,稱為有向邊或弧(arc)。
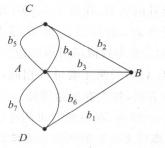 圖6
圖6所有邊都是無向邊的圖稱為 無向圖(graph或undirected graph),所有邊都是有向邊的圖稱為 有向圖(digraph或directed graph)。
③圖的拓撲不變性質。需要注意的是,我們討論的圖不但與節點位置無關,而且與邊的形狀和長短也無關。
若有一條邊連一個圖的某兩個節點,則稱這兩個節點 相鄰,並稱這兩個節點為這條邊的端點;若某一節點是某一條邊的端點,則稱這個節點和這條邊關聯;若兩條邊和同一節點關聯,則稱這兩條邊相鄰;兩個端點是同一個節點的邊稱為 環;若某條邊的兩個端點不是同一個節點,且只有一條邊連這兩個節點,則稱這條邊為 桿。
只有一個節點而沒有邊的圖稱為 平凡圖;沒有邊的圖稱為 孤立圖;以某兩節點為端點的邊可能不止一條,這時稱連這兩個節點的邊為重邊,既可以有環,也可以有重邊的圖稱為 準圖;沒有環而可能有重邊的圖稱為 帶重圖;沒有重邊而可能有環的圖稱為 帶環圖;既沒有重邊也沒有自環的圖稱為 簡單圖;若一個圖的階是有限的,則稱這個圖為 有限圖,否則稱這個圖為 無限圖;每兩個節點都相鄰的簡單圖稱為 完全圖;若一個n階圖的節點用1,2,…,n來代表,則稱它為 標定圖;若在圖的每一條邊上賦以一個實數或者對於每個節點賦以一個實數,則稱它為 賦權圖。