正文
所謂篩法，可描述如下：①給定“被篩集合”。這是依賴於某一參數x 的集合族A(x)，x∈x。每一集合A(x)由有限個（可重複的）整數組成，且當x →∞時元素個數也趨於無窮。②給定“篩”。這是由無限多個不同的素數組成的集合p 以及對每一p ∈p 給定h(p)個模p的不同的剩餘類H(p)所組成，其中1≤h(p)<p。③進行“篩選”。給定正數z>2，把集合A(x)中屬於剩餘類H(p)的所有元素都去掉，其中p≤z,p∈p。剩下的元素所組成的A(x)的子集及其元素個數，均記為S(A(x)，H(p),p,z),是x和z的函式,稱之為篩函式。當H(p)僅有一個剩餘類n呏0(modp)時，篩函式記為S(A(x)，p,z)。
選取不同的被篩集合、篩和z,經篩選後，可得到具有不同算術性質的子集，所以許多數論問題有可能用篩法來研究。例如，取參數x為正整數N，A(N)由某些大於1不超過N的整數組成,p是全體素數。再取z=
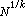（整數k≥2）。於是S(A(N)，p,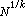)是由A(N)中所有大於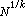不超過N，且其素因子都大於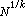的整數組成。這種整數是不超過k-1個素因數的乘積。當k=2時即是埃拉托斯特尼篩法。 又如,設r、s是正整數。以｛r,s｝表示命題：每個充分大的偶數是兩個素因數分別不超過r和s個的乘積之和。命題｛1，1｝基本上就是哥德巴赫猜想。對於這類命題，可取參數x為偶數N，集合A1(N)={n(N-n),2≤n≤N-2}，p為全體素數，z=
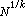（整數k≥2）。若能證明對充分大的偶數N 有S(A1(N )，p,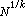)>0，則證明了命題{k-1,k-1}。假若將A1(N)改取為集合A2(N)={N-p,素數p<N},那么,根據對充分大的偶數N有
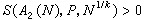,就可推出命題｛1,k-1｝。 篩法理論主要是研究篩函式的性質，特別是它的上、下界估計。按照h(p)/p在某種平均意義上是“小”還是“大”，就稱相應的篩法為小篩法或大篩法。以上的例子都是小篩法。大篩法是ю.B.林尼克在研究模p的正的最小二次非剩餘時提出來的。 他證明了對任意的篩p和H(p)，只要
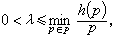
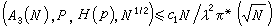，這裡A3(N)={M+n,1≤n≤N },с1是一正常數,π
(y)是p中不超過y的素數個數。由於h(p)≥λp是“很大”的，所以林尼克把他的方法稱之為大篩法。 小篩法雖然歷史悠久，但是在數論的具有重要理論價值的研究中，一直沒有得到套用，這主要是由於用它來得到篩函式所需要的上界估計、尤其是正的下界估計十分困難。1920年左右，V.布龍首先對埃拉托斯特尼篩法作了改進，證明了命題｛9,9｝成立,以及所有孿生素數的倒數組成的級數是收斂的，開闢了套用篩法研究數論的新途徑。他的方法稱為布龍法。40年代，B.J.羅塞改進了布龍篩法，提出了所謂羅塞篩法，但是大約20年後才為人注意。這兩種小篩法理論具有很強的組合數特徵，所以又稱為組合篩法。1950年左右，A.賽爾伯格利用二次型求極值的方法對埃拉托斯特尼篩法又作了重大改進，他的方法稱為賽爾伯格（上界）篩法，十分簡單，便於套用。小篩法在研究命題{r，s}和算術級數中的素數分布（即布龍－蒂奇馬什定理）等許多著名數論問題時，得到了豐富的成果和自身的進一步發展。對小篩法理論作出重要貢獻的還有A.A.布克什塔布引入了組合方法與P.庫恩引入了加權方法。小篩法本身是初等的，但是必需同高深的分析方法相結合才能套用於某些問題的研究，例如命題{1,s}的研究。W.B.朱爾卡特和H.-E.里歇、H.伊瓦尼克等人利用現有的小篩法理論，只在最簡單的情形得到了篩函式的最佳估計。小篩法理論的發展還遠遠沒有完結。
A.雷尼首先於1947年改進了大篩法。1965年，K.F.羅特和E.邦別里又作了重大的改進，雷尼用他的方法估計狄利克雷L函式的零點密度,並結合布龍篩法證明了命題{1,b)}，這裡b)是一個未定出的大常數，開闢了套用大篩法的新途徑。E.邦別里發現大篩法可歸結為估計指數和的平方均值
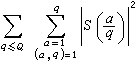
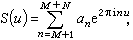
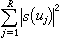
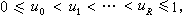
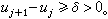大篩法上界估計的證明一直是比較複雜的，1967年，P.X.加拉格爾用極為初等的微積分方法給出一個十分簡單的證明。1974年，H.L.蒙哥馬利和R.C.沃恩利用泛函分析的對偶原理把大篩法歸結為某種雙線性型的估計，證明了最佳估計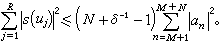 
中國的數學家在小篩法和大篩法的理論及其套用方面都有重要貢獻。1957年，王元證明了命題｛2，3｝。1962年，潘承洞證明了命題｛1，5｝。1966年，陳景潤證明了命題｛1，2｝（證明全文於1973年發表），世界公認是篩法理論最卓越的套用成果，陳景潤在他的一些重要工作中所提出的思想和方法，對近代小篩法的進展有重要的影響。
參考書目
H.Halberstam and H.-E.Richert,Sieve Methods,Academic Press，London. 1974. Y.Motohashi，Lectures on Sieve Methods and Prime Number Theorems, Springer-Verlag, Berlin,1984.
配圖
相關連線
王敏:哥德巴赫猜想的初等數學的證明
見本網的哥德巴赫猜想欄
