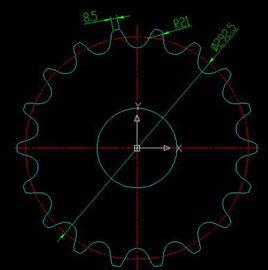
節圓、節點、節線
節圓:兩齒輪連心線上咬合接觸點各齒輪上留下軌跡稱為節圓,它的直徑就是節圓直徑。再簡單一點說,節圓直徑是兩個齒輪的交接點(切點)。對於一個單一的齒輪來說是不存在節圓的。而且兩齒輪節圓的大小顯然是隨其中心距的變化而變化的。
節點:一對漸開線齒廓不論在哪一點嚙合傳動,其嚙合點的公法線必與這對齒輪的連心線交於一定點,這個定點就是節點 。
接線:一對齒廓嚙合過程中節點在齒輪上的軌跡稱為節線。
節圓直徑的計算公式
節圓直徑的計算公式:d2=2A/(i+1),其中A-中心距, i-速比Z2/Z1, 嚙合角conα=A0/A(conα0).其中A0-非變位嚙合時的中心距,A-變位後的中心距,α0-非變位壓力角(20°)。如果標準齒輪那是很容易的,節圓直徑就等於分度圓直徑d=mZ,嚙合角就是20°(或14.5°) 。
節圓半徑的計算
節圓直徑是齒輪的一個重要參數,齒輪上的很多數據都是與節圓直徑有關的。比如:齒數*模數=分度圓直徑。
對外嚙合齒輪(變位和非變位齒輪):
節圓半徑=中心距*齒數/齒數和
對內嚙合齒輪(變位和非變位齒輪):
節圓半徑=中心距*齒數/齒數差
節圓在齒輪不變位時也等於分度圓。
基圓與分度圓
基圓:就是生成漸開線的那個圓。通俗的講,就是一根細線纏在基圓上,把這根線逐漸展開,其端點的軌跡形成該基圓的漸開線。
分度圓:齒輪的分度圓是一大小完全確定的圓,不論這個齒輪是否與另一齒輪嚙合,也不論兩輪的中心距如何變化,每個齒輪都有一個唯一的大小完全確定的分度圓。
節圓和分度圓的關係
節圓和分度圓的關係:在標準中心距條件下嚙合的一對漸開線齒輪,其節圓與分度圓重合;在非標準中心距條件下嚙合時,其節圓與分度圓不重合。節圓只有嚙合時才“存在”,而分度圓各個齒輪都存在。分度圓一個虛擬的圓。