等距對應簡介
若兩個曲面的點之間存在一一對應,使它們上面的對應曲線有相同的弧長,則稱這兩個曲面是等距的,或稱兩曲面等距等價,這樣的對應稱為等距對應,而一個曲面到另一個曲面的這樣的映射稱為等距映射。特別地,將一個曲面到自身的等距映射稱為等距變換,曲面在等距映射下不變的幾何量稱為曲面的等距不變數或內蘊量。在等距映射下,不變的幾何性質稱為曲面的等距性質或內蘊性質(也稱內在性質)。等距映射的一種具體刻畫是把一個曲面經過保持曲面上所有曲線長度不變的變形變成另外一個曲面。因此,一般地也把這類等距稱為彎曲形變,而把等距的曲面稱為可以貼合的曲面。
局部等距對應
對於兩張對應的曲面,若它們對應著的弧段總是具有相等的弧長長度,則稱這個對應是兩張曲面之間的一個局部等距對應,稱這兩張曲面是局部等距的。若兩張曲面之間的局部等距對應是整體一一對應,則該對應就是一個等距對應,稱這兩張曲面是等距的。等距與局部等距的區別,可從觀察平面與圓柱面之間的聯繫和區別入手,進行思考。
充要條件
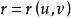 等距對應
等距對應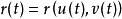 等距對應
等距對應設曲面的方程為 ,那么曲面上曲線c在空間中的方程為: 。
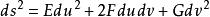 等距對應
等距對應若以S表示曲面上曲線的弧長, ,是關於微分du、dv的一個二次形式,稱為曲面的第一基本形式,它的係數E、F、G稱為曲面的第一基本量。
兩個曲面可建立等距對應的充要條件是選取適當的參數後,它們有相同的第一基本形式在給出兩個曲面的方程後,證明兩個曲面成等距對應時,先給一個等距對應式,這樣只需根據兩曲面的方程,求出其第一基本形式,然後通過等距變換式,驗證此兩個曲面有相同的第一基本形式。
套用
弧齒錐齒輪在機械航空動力傳輸領域具有廣泛的套用,其嚙合理論和製造技術一直是各國專家學者研究的熱點。20世紀90年代起,隨著計算機數值計算方法的發展,輪齒接觸分析(TCA)技術逐漸得到套用。TCA能提供輪齒接觸的豐富信息,成為齒輪嚙合性能預控設計不可或缺的手段。藉助TCA方法,方宗德等發展了“局部綜合”法,預置在參考點2階接觸參數,以期對輪齒傳動誤差和齒面印痕進行控制。唐進元等提出了TCA的改進算法,使TCA的求解方法更加實用;並進一步發展了基於預定嚙合特性的點嚙合齒面設計方法,蘇進展、方宗德又進一步利用TCA的方法完成了對弧齒錐齒輪接觸印痕穩定性與誤差敏感性的最佳化設計與試驗研究。
魏冰陽等提出了一種基於Ease-off曲面等距變換的輪齒嚙合仿真分析方法。利用曲面曲撓參數,給出了2階密切曲面的定義及其拓撲方法;在2階微分精度範圍內,密切曲面與原曲面貼近,可以代替散曲面做幾何解析。利用空間坐標變換,建立了弧齒錐齒輪加工的嚙合方程和通用產成模型。基於嚙合等距對應原理,求解齒面對應點的離差;利用最小二乘法,拓撲散曲面,構建Ease-off差齒面的2階密切曲面。基於Ease-off密切曲面參數,利用齒面接觸的等距線、漸近方向,解析出齒面接觸位形、接觸路徑、傳動誤差等嚙合性能參數。分析結果表明:一次性構建Ease-off的2階密切曲面,能夠獲得輪齒完備的嚙合信息,曲面拓撲精度可到達0.1μm;與現行的嚙合仿真方法相比易於齒面反求、數值計算,嚙合信息的獲得也更為便捷。

