等價分解

等價分解是函式分解論中討論分解惟一性時的重要概念。分解惟一性是函式分解論中研究的重要性質之一。

簡介

等價分解是函式分解論中討論分解惟一性時的重要概念。

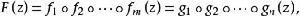等價分解

等價分解

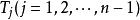等價分解

設F(z)為一超越整函式，具有兩個非平凡分解： 若m=n及存在有n-1個雙線性函式 使得 則稱上述分解為等價的。

分解惟一性

分解惟一性是函式分解論中研究的重要性質之一。若一亞純函式F(z)的任兩個非平凡分解皆為等價時，則稱F具有分解惟一性。

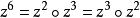等價分解

等價分解

由於 為明顯的兩個非等價的分解，所以為避免混淆及複雜性，現考慮因子皆為超越整函式，並且因子為素的情形來討論分解惟一性，即F(z)為一超越整函式且F可表為 其中f及g等皆為超越的素整函式，若上述兩種分解等價，則稱F具有分解惟一性。

雙線性函式

（bilinear function ）

雙線性函式是線性函式的推廣。設V，V是域P上的線性空間，V×V到P的雙線性映射φ稱為V×V上的雙線性函式。特別地，當V=V=V時，φ稱為V上的雙線性函式。

半雙線性函式（sesquilinear function）是雙線性函式的推廣。