定義介紹
在數學中,特別是線性代數和泛函分析里,一個矩陣或線性運算元的 極分解是一種類似於複數之極坐標分解的分解方法。一個複數 z可以用它的模長和輻角表示為:
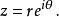 極分解
極分解 極分解
極分解其中 r是 z的模長(因此是一個正實數),而則為 z的輻角。
矩陣的極分解
一個復係數矩陣 A的 極分解將其分解成兩個矩陣的乘積,可以表示為:
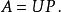 極分解
極分解其中 U是一個酉矩陣, P是一個半正定的埃爾米特矩陣。這樣的分解對任意的矩陣 A都存在。當 A是可逆矩陣時,分解是唯一的,並且 P必然為正定矩陣。注意到:
 極分解
極分解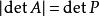 極分解
極分解 極分解
極分解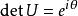 極分解
極分解可以看出極分解與複數的極坐標分解的相似之處:P對應著模長(
),而U則對應著輻角部分()。矩陣P可以由
 極分解
極分解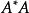 極分解
極分解 極分解
極分解得到,其中 A* 表示矩陣 A的共軛轉置。由於 為半正定的埃爾米特矩陣,它的平方根唯一存在,所以這個式子是有意義的。而矩陣 U可以通過表達式得到。
當對矩陣 A進行奇異值分解得到 A = W Σ V後,可以因而導出其極分解:
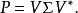 極分解
極分解 極分解
極分解可以看到導出的矩陣 P是正定矩陣,而 U是酉矩陣。
對稱地,矩陣 A也可以被分解為:
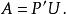 極分解
極分解這裡的 U仍然是原來的酉矩陣,而 P′ 則等於:
 極分解
極分解這個分解一般被稱為 左極分解,而文章開頭介紹的分解被稱為 右極分解。左極分解有時也被稱為 逆極分解。
矩陣 A是正規的若且唯若 P′ = P。這時候 UΣ = ΣU,並且 U可以用與 Σ交換的酉對稱矩陣 S進行酉對角化,這樣就有 S U S*= Φ,其中 Φ是一個表示輻角的酉對角矩陣 e。如果設 Q = V S,那么極分解就可以被改寫為:
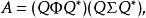 極分解
極分解因此矩陣 A有譜分解:
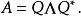 極分解
極分解其中的特徵值為複數, ΛΛ= Σ。
將 A射到其極分解里的酉部分 U是一個從一般線性群GL( n, C) 射到酉群U( n) 的映射。這是一個同倫等價,因為所有正定矩陣構成的空間是一個可縮空間。實際上,U( n) 是 GL( n, C) 的極大緊子群。
有界運算元
從復希爾伯特空間到復希爾伯特空間的有界線性運算元 A的 極分解,是將其正則分解為一個準等距變換和一個半正定運算元的乘積。
矩陣的極分解被推廣為:如果 A是一個有界線性運算元,那么可以將其唯一地分解為乘積 A= UP,其中 U是一個準等距變換,而 P是一個半正定的自伴運算元,並且 U的定義空間覆蓋 P的像集。
無界運算元
如果 A是復希爾伯特空間之間的閉稠定無界運算元,那么仍然有惟一的 極分解
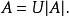 極分解
極分解這裡 | A| 是一個(可能無界)非負自伴運算元,與 A有相同的定義域, U是一個在值域 Ran(| A|) 的正交補上為 0 的部分等距。
用上面同樣的引理,在無界運算元同樣一般地成立。如果 Dom( A*A) = Dom( B*B) 和 A*Ah= B*Bh對所有 h∈ Dom( A*A) 成立,那么存在一個部分等距 U使得 A= UB。如果 Ran( B)⊂ Ker( U),則 U是惟一的。運算元 A是閉稠定的保證了運算元 A*A是自伴的(有同樣的定義域),從而我們可以定義( A*A)。 利用引理便給出了極分解。
如果一個無界運算元 A是對馮·諾依曼代數 M的affiliated operator,且 A= UP是其極分解,那么 U在 M中從而是 P, 1( P) 對任何 [0, ∞) 中 Borel 集 B的譜投影。
套用
連續介質力學中使用極分解來將形變分解成拉伸和旋轉的部分,其中 P表示拉伸的部分, U表示旋轉的部分。
相關條目
•奇異值分解
•矩陣分解
•Cartan分解
•岩澤分解

