後來,古希臘數學家歐多克斯(Eudoxus of Cnidus, 408-355 BC)改進了安提芬的窮竭法。將其定義為:“在一個量中減去比其一半還大的量,不斷重複這個過程,可以使剩下的量變得任意小”。
古希臘數學家阿基米德進一步完善了“窮竭法”,並將其廣泛套用於求解曲面面積和鏇轉體體積。阿基米德最早使用窮竭法進行了積分運算,是微積分學的先驅。窮竭法被後人稱為阿基米德原理。
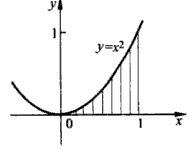
例如,計算y=x^2與x軸在x=0和x=1之間圍成的曲邊三角形的面積,把底邊[0,1]分成n等分,分點分別是1/n,2/n,…(n-1)/n,然後在每個分點處作底邊的垂線,這樣曲邊三角形被分成了n個窄條,對每個窄條,近似用矩形條替代。每個矩形的底寬1/n,高(i/n)^2(i=0,1,2,…,n-1),把這些矩形條加起來,得到S的近似Sn:
Sn=0·(1/n)+(1/n)^2·(1/n)+(2/n)^2·(1/n)+…+[(n-1)/n]^2·(1/n)=1/n^3·[n(n-1)(2n-1)/6]=1/6·(1-1/n)(2-1/n)
對每個n,都可以算出相應的Sn的值,一方面,隨著n的增大Sn的值,來越接近S.但另一方面,所得的Sn始終都是S的近似值,為了得到S的精確值,使n無限制的增大,從幾何上看,面積Sn的那個多邊形越來越貼近曲邊三角形,即阿基米德所說的窮竭曲邊三角形,從數值上看,Sn無限接近一個確定的數,這個數就是曲邊三角形的面積S,這個數等於1/3,當年,阿基米德就是通過這個方法求得結果.
用窮竭法計算曲邊形的面積時,對不同的曲邊形,採用不同的直邊形去逼近。並且計算的過程中採用了特殊的技巧,因而不具有一般性,無法向一般的曲邊形推廣.
