基本介紹
軸反射變換簡稱軸反射,是歐氏幾何中一種重要變換。在歐氏平面上或歐氏空間中,把任一點A映成關於給定直線S對稱的點A′的變換稱為關於直線S的軸反射變換,直線S稱為反射軸。平面軸反射是第二種正交變換,空間軸反射變換亦稱半周旋轉,它是旋轉角為π的空間繞反射軸的旋轉,因而是第一種正交變換。在軸反射變換下,連結每一對對應點A,A′所得到的線段都垂直於S,且被S所平分。反射軸上的每一點都是不動點,在平面直角坐標系中,若以x軸為反射軸,則軸反射的代數表達式為
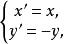 空間軸反射變換
空間軸反射變換 其中(x,y),(x′,y′)分別是變換前的點與它的對應點的坐標。
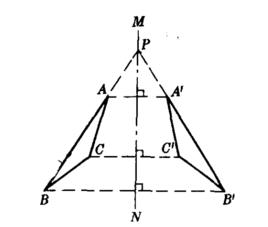
軸反射(軸對稱,半周旋轉) 在旋轉變換中,旋轉的角可能是180°,於是第一圖形上任意一點M的對應點,將是M對於它在軸上的射影m的對稱點M'(圖1) 。
繞一直線作180°的旋轉,叫做對於這直線的反射或軸反射(或軸對稱,或半周旋轉)。
這時,不需指出軸的指向,軸反射是自逆的,就是說,用同樣的作法於求得的點M',便重新回到點M。.
由上面所說可知:可由軸反射互得的兩個圖形是全等的 。
空間的軸對稱變換是空間的等距變換的特殊情形,因此,空間等距變換的所有一般性質,對於空間的軸對稱變換都是正確的 。
空間正交變換的分解
空間正交變換的分解是空間契約(正交)變換的重要特徵之一,空間中任何契約變換都可以分解為若干平面反射之積,而且積中因子可以不超過四個。如果契約變換能表成偶數個平面反射之積,則是一個運動變換。如果契約變換能表成奇數個平面反射之積,則是一個第二種契約變換。具體地:
1.麼變換是任何一個平面反射與自身的積。
2.平移是兩個反射面平行且垂直於平移方向的平面反射之積,兩反射面的距離是平移距離的一半。
3.旋轉是兩個反射面相交於旋轉軸的平面反射之積,兩反射面的夾角是旋轉角的一半,軸反射是半周旋轉,可分解為反射面相交於對稱軸且互相垂直的兩個平面反射之積。
4.螺旋運動是旋轉與平移的積,因而可分解為四個平面反射之積,其中兩個表示旋轉,兩個表示平移。
5.旋轉反射是旋轉與平面反射之積,因而可分解為三個平面反射之積,其中兩個之積表示旋轉。
6.滑行反射是平移與平面反射之積,因而可分解為三個平面反射之積,其中有兩個之積表示平移 。