介紹
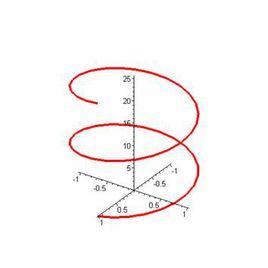
 DNA的雙螺旋結構
DNA的雙螺旋結構我們所接觸到的空間,大至宇宙,小至細胞,其中都充滿著五光十色、變幻紛雜的曲線。諸如太陽系行星的軌道,飛機的航道,盤山蜿蜒的公路,沙發里的彈簧,織物圖案花紋,齒輪和凸輪的輪廓,生命遺傳物質DNA的雙螺旋結構,等等。
在人們接觸到的曲線中,最簡單的要算是直線和圓了。這些曲線是初等平面幾何中討論的對象。其次較為複雜的曲線是二次曲線,即橢圓、雙曲線和拋物線。這些已經在平面解析幾何里學習過,討論的方法是用坐標和一元二次代數方程。
對於更複雜的曲線,僅僅用初等代數一般是不能解決問題的。研究更加一般的光滑曲線的幾何性質,微積分則是有力的工具。我們可以用微積分來推導三個刻劃一條空間曲線幾何性質的基本幾何量,就是弧長、曲率和撓率。
表示式
參數方程
一條空間曲線的表示式是
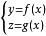 空間曲線
空間曲線或
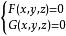 空間曲線
空間曲線每一組方程都是把一條空間曲線作為兩個曲面的交線,用上述表示式研究空間曲線會引起形式不對稱和計算繁瑣的缺點。為了避免這些缺點,我們經常採用參數方程:
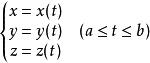 空間曲線
空間曲線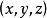 空間曲線
空間曲線 空間曲線
空間曲線表示一條空間曲線,其中 表示曲線上一點在右手系直角坐標系下的坐標, 為參數。
 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線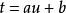 空間曲線
空間曲線如果把 看成時間,那么該曲線可以看成是空間質點從時刻 到 之間的運動軌跡。不過一般而言, 不具備這個物理意義,而且參數的選擇並不是唯一的。例如對於參數變換 ,參數方程的各函式將改變形式而曲線本身形狀並不改變。
向量方程
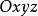 空間曲線
空間曲線 空間曲線
空間曲線設右手直角坐標系中的坐標基向量為,我們可以將曲線的參數方程寫成向量方程:
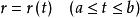 空間曲線
空間曲線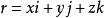 空間曲線
空間曲線式中代表曲線上點的位置向量。
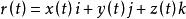 空間曲線
空間曲線 空間曲線
空間曲線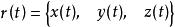 空間曲線
空間曲線稱為關於變數的向量函式,常簡寫成分量表示。
三個元素
弧長
設一空間曲線決定於參數方程
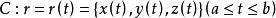 空間曲線
空間曲線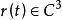 空間曲線
空間曲線式中各函式有直至三階的連續導數,即。
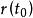 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線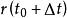 空間曲線
空間曲線設是曲線上的任意點,簡稱點。是其鄰點。這兩點決定一個向量,即:
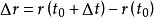 空間曲線
空間曲線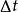 空間曲線
空間曲線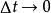 空間曲線
空間曲線 空間曲線
空間曲線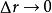 空間曲線
空間曲線除以便得到方向相同而長度不同的向量。當時,從曲線的連續性可知,而且
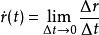 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線是曲線在點的一個切向量。
 空間曲線
空間曲線 空間曲線
空間曲線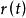 空間曲線
空間曲線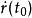 空間曲線
空間曲線 空間曲線
空間曲線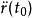 空間曲線
空間曲線當變動時,曲線可以看成質點的軌跡,的物理意義就是質點在點的速度向量,則是加速度向量。
 空間曲線
空間曲線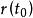 空間曲線
空間曲線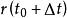 空間曲線
空間曲線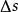 空間曲線
空間曲線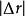 空間曲線
空間曲線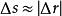 空間曲線
空間曲線設曲線的兩鄰點和之間的弧長為,對應的弦長為,有,從而得到
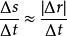 空間曲線
空間曲線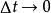 空間曲線
空間曲線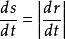 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線當時,便可得到,對該式從到積分得到
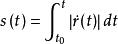 空間曲線
空間曲線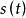 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線稱為曲線從到的弧長,上式也可用分量形式表示為
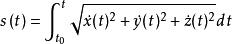 空間曲線
空間曲線曲率
 空間曲線
空間曲線對於一條空間曲線,採用自然參數表示的方程
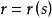 空間曲線
空間曲線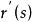 空間曲線
空間曲線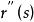 空間曲線
空間曲線其一階導數表示曲線的單位切向量,我們進一步考慮它的二階導數,給出如下定義:
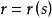 空間曲線
空間曲線 空間曲線
空間曲線空間曲線在點的曲率為
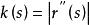 空間曲線
空間曲線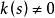 空間曲線
空間曲線當時,其倒數
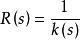 空間曲線
空間曲線 空間曲線
空間曲線稱為曲線在點的曲率半徑。
撓率
 空間曲線
空間曲線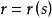 空間曲線
空間曲線 空間曲線
空間曲線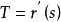 空間曲線
空間曲線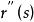 空間曲線
空間曲線 空間曲線
空間曲線 空間曲線
空間曲線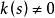 空間曲線
空間曲線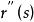 空間曲線
空間曲線曲線關於其弧長的一階導數是單位切向量,但是二階導數一般並不是單位向量函式,因為其長度即曲線在該點的曲率一般不等於1,但是二階導數垂直,當時,我們把規範化為單位向量,即
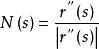 空間曲線
空間曲線 空間曲線
空間曲線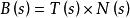 空間曲線
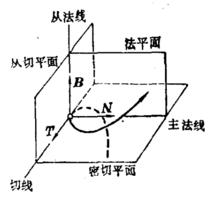
空間曲線稱為曲線在點的主法向量,而且稱為曲線在同一點的從法向量。
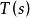 空間曲線
空間曲線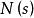 空間曲線
空間曲線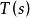 空間曲線
空間曲線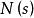 空間曲線
空間曲線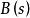 空間曲線
空間曲線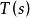 空間曲線
空間曲線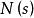 空間曲線
空間曲線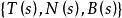 空間曲線
空間曲線由於垂直,且和都是單位向量,從而是垂直於和的單位向量。由此我們在曲線上任意點獲得一組兩兩正交的單位向量組。這樣與曲線緊密聯繫的三個向量形成了一個單位正交標架。
 空間曲線
空間曲線不落在同一平面上的空間曲線,我們稱之為撓曲線。如同彎曲的概念一樣,曲線論中也有“撓扭”的概念,用於描述一條曲線在一點偏離密切平面的程度。為了描述這種偏離度,我們將用到密切平面的變化率,也就是密切平面的法向量的變化率,這樣就導出曲線的“撓率”這一概念。
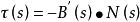 空間曲線
空間曲線 空間曲線
空間曲線定義稱為曲線在點處的撓率。顯然平面曲線的撓率恆為零。