魯棒性
魯棒是Robust的音譯，也就是健壯和強壯的意思。它是在異常和危險情況下系統生存的關鍵。比如說，計算機軟體在輸入錯誤、磁碟故障、網路過載或有意攻擊情況下，能否不當機、不崩潰，就是該軟體的魯棒性。所謂“魯棒性”，是指控制系統在一定（結構，大小）的參數攝動下，維持其它某些性能的特性。根據對性能的不同定義，可分為穩定魯棒性和性能魯棒性。以閉環系統的魯棒性作為目標設計得到的固定控制器稱為魯棒控制器。
穩定魯棒控制
魯棒控制（Robust Control）方面的研究始於20世紀50年代。在過去的20年中，魯棒控制一直是國際自控界的研究熱點。所謂“魯棒性”，是指控制系統在一定（結構，大小）的參數攝動下，維持某些性能的特性。根據對性能的不同定義，可分為穩定魯棒性和性能魯棒性。以閉環系統的魯棒性作為目標設計得到的固定控制器稱為魯棒控制器。
由於工作狀況變動、外部干擾以及建模誤差的緣故，實際工業過程的精確模型很難得到，而系統的各種故障也將導致模型的不確定性，因此可以說模型的不確定性在控制系統中廣泛存在。如何設計一個固定的控制器，使具有不確定性的對象滿足控制品質，也就是魯棒控制，成為國內外科研人員的研究課題。
主要的魯棒控制理論有：（1）Kharitonov區間理論；（2）H∞控制理論；（3）結構奇異值理論（μ理論）等等。
被控對象的不確定性對各種控制方法都提出了魯棒性的要求，有各種各樣的衡量系統魯棒性的指標，魯棒穩定性就是其中的一種。
系統的魯棒穩定性指的是由一個不確定性對象構成的閉環控制系統，其閉環極點能否確保在某個指定的d域內變化，而不會因為對象的結構或參數變化而跑到D域外面去。
為了表征系統的D魯棒穩定性，不斷有人提出新的判定方法和測試函式。但是，到目前為止，還是提出的D魯棒穩定性測試函式F(ω)的計算量最小，最便於套用。
詳細介紹
溯源和背景
魯棒性/抗變換性（英文：robustness）原是統計學中的一個專門術語，20世紀70年代初開始在控制理論的研究中流行起來，用以表征控制系統對特性或參數擾動的不敏感性。鑒於中文“魯棒性”的詞義不易被理解，“robustness”又被翻譯成了語義更加易懂的“抗變換性”，“抗變換性”和“魯棒性”在譯文中經常互相通用。
通信網路的魯棒性在實際問題中，系統特性或參數的攝動常常是不可避免的。產生攝動的原因主要有兩個方面，一個是由於量測的不精確使特性或參數的實際值會偏離它的設計值（標稱值），另一個是系統運行過程中受環境因素的影響而引起特性或參數的緩慢漂移。因此，魯棒性已成為控制理論中的一個重要的研究課題，也是一切類型的控制系統的設計中所必須考慮的一個基本問題。對魯棒性的研究主要限於線性定常控制系統，所涉及的領域包括穩定性、無靜差性、適應控制等。
原理
魯棒性問題與控制系統的相對穩定性（頻率域內表征控制系統穩定性裕量的一種性能指標）和不變性原理（自動控制理論中研究扼制和消除擾動對控制系統影響的理論）有著密切的聯繫，內模原理（把外部作用信號的動力學模型植入控制器來構成高精度反饋控制系統的一種設計原理）的建立則對魯棒性問題的研究起了重要的推動作用。當系統中存在模型攝動或隨機干擾等不確定性因素時能保持其滿意功能品質的控制理論和方法稱為魯棒控制。早期的魯棒控制主要研究單迴路系統頻率特性的某些特徵，或基於小攝動分析上的靈敏度問題。現代魯棒控制則著重研究控制系統中非微有界攝動下的分析與設計的理論和方法。
控制系統的一個魯棒性是指控制系統在某種類型的擾動作用下，包括自身模型的擾動下，系統某個性能指標保持不變的能力，即抗干擾能力較強。對於實際工程系統，人們最關心的問題是一個控制系統當其模型參數發生大幅度變化或其結構發生變化時能否仍保持漸近穩定，這叫穩定魯棒性。進而還要求在模型擾動下系統的品質指標仍然保持在某個許可範圍內，這稱為品質魯棒性。魯棒性理論致力於研究多變數系統具有穩定魯棒性和品質魯棒性的各種條件。它的進一步發展和套用，將是控制系統最終能否成功套用於實踐的關鍵。
在數字水印技術中，魯棒性是指在經過常規信號處理操作後能夠檢測出水印的能力；針對圖像的常規操作包括空間濾波、有損壓縮、列印與複印、幾何變形等；
魯棒控制理論
魯棒性（robustness）就是系統的健壯性。它是在異常和危險情況下系統生存的關鍵。比如說，計算機軟體在輸入錯誤、磁碟故障、網路過載或有意攻擊情況下，能否不當機、不崩潰，就是該軟體的魯棒性。所謂“魯棒性”，是指控制系統在一定（結構，大小）的參數攝動下，維持某些性能的特性。根據對性能的不同定義，可分為穩定魯棒性和性能魯棒性。以閉環系統的魯棒性作為目標設計得到的固定控制器稱為魯棒控制器。
魯棒控制是一個著重控制算法可靠性研究的控制器設計方法。魯棒性一般定義為在實際環境中為保證安全要求控制系統最小必須滿足的要求。一旦設計好這個控制器，它的參數不能改變而且控制性能保證。
魯棒控制方法，是對時間域或頻率域來說，一般假設過程動態特性的信息和它的變化範圍。一些算法不需要精確的過程模型但需要一些離線辨識。
一般魯棒控制系統的設計是以一些最差的情況為基礎，因此一般系統並不工作在最優狀態。
魯棒控制方法適用於穩定性和可靠性作為首要目標的套用，同時過程的動態特性已知且不確定因素的變化範圍可以預估。飛機和空間飛行器的控制是這類系統的例子。
過程控制套用中，某些控制系統也可以用魯棒控制方法設計，特別是對那些比較關鍵且（1）不確定因素變化範圍大；（2）穩定裕度小的對象。
但是，魯棒控制系統的設計要由高級專家完成。一旦設計成功，就不需太多的人工干預。另一方面，如果要升級或作重大調整，系統就要重新設計。
通常，系統的分析方法和控制器的設計大多是基於數學模型而建立的，而且，各類方法已經趨於成熟和完善。然而，系統總是存在這樣或那樣的不確定性。在系統建模時，有時只考慮了工作點附近的情況，造成了數學模型的人為簡化；另一方面，執行部件與控制元件存在製造容差，系統運行過程也存在老化、磨損以及環境和運行條件惡化等現象，使得大多數系統存在結構或者參數的不確定性。這樣，用精確數學模型對系統的分析結果或設計出來的控制器常常不滿足工程要求。近些年來，人們展開了對不確定系統魯棒控制問題的研究，並取得了一系列研究成果。Hoo魯棒控制理論和μ分析理論則是當前控制工程中最活躍的研究領域之一，多年來一直備受控制研究工作者的青睞。作者通過系統地研究線性不確定系統、時間滯後系統、區間系統、離散時間系統的魯棒穩定性問題，提出了有關係統魯棒穩定性的分析和設計方法。
漸近穩定
以漸近穩定為性能指標的一類魯棒性。如果控制系統在其特性或參數的標稱值處是漸近穩定的，並且對標稱值的一個鄰域內的每一種情況它也是漸近穩定的，則稱此系統是結構漸近穩定的。結構漸近穩定的控制系統除了要滿足一般控制系統設計的要求外，還必須滿足另外一些附加的條件。這些條件稱為結構漸近穩定性條件，可用代數的或幾何的語言來表述，但都具有比較複雜的形式。結構漸近穩定性的一個常用的度量是穩定裕量，包括增益裕量和相角裕量，它們分別代表控制系統為漸近穩定的前提下其頻率回響在增益和相角上所留有的儲備。一個控制系統的穩定裕量越大，其特性或參數的允許攝動範圍一般也越大，因此它的魯棒性也越好。業已證明，線性二次型(LQ)最優控制系統具有十分良好的魯棒性，其相角裕量至少為60°，並確保1/2到∞的增益裕量。已經成為軟體性能指標之一。
H∞控制理論
H∞控制理論是20世紀80年代開始興起的一門新的現代控制理論。H∞控制理論是為了改變近代控制理論過於數學化的傾向以適應工程實際的需要而誕生的,其設計思想的真髓是對系統的頻域特性進行整形(Loopshaping),而這種通過調整系統頻率域特性來獲得預期特性的方法,正是工程技術人員所熟悉的技術手段,也是經典控制理論的根本。
1981年Zames首次用明確的數學語言描述了H∞最佳化控制理論,他提出用傳遞函式陣的H∞範數來記述最佳化指標。1984年加拿大學者Fracis和Zames用古典的函式插值理論提出了H∞設計問題的最初解法,同時基於運算元理論等現代數學工具,這種解法很快被推廣到一般的多變數系統,而英國學者Glover則將H∞設計問題歸納為函式逼近問題,並用Hankel運算元理論給出這個問題的解析解。Glover的解法被Doyle在狀態空間上進行了整理並歸納為H∞控制問題,至此H∞控制理論體系已初步形成。
在這一階段提出了H∞設計問題的解法,所用的數學工具非常繁瑣,並不像問題本身那樣具有明確的工程意義。直到1988年Doyle等人在全美控制年會上發表了著名的DGKF論文,證明了H∞設計問題的解可以通過適當的代數Riccati方程得到。DGKF的論文標誌著H∞控制理論的成熟。迄今為止,H∞設計方法主要是DGKF等人的解法。不僅如此,這些設計理論的開發者還同美國的The Math Works公司合作,開發了MATLAB中魯棒控制軟體工具箱(Robust Control Toolbox),使H∞控制理論真正成為實用的工程設計理論。
研究
魯棒控制的早期研究，主要針對單變數系統（SISO）的在微小攝動下的不確定性，具有代表性的是Zames提出的微分靈敏度分析。然而，實際工業過程中故障導致系統中參數的變化，這種變化是有界攝動而不是無窮小攝動。因此產生了以討論參數在有界攝動下系統性能保持和控制為內容的現代魯棒控制。
現代魯棒控制是一個著重控制算法可[1]靠性研究的控制器設計方法。其設計目標是找到在實際環境中為保證安全要求控制系統最小必須滿足的要求。一旦設計好這個控制器，它的參數不能改變而且控制性能能夠保證。
魯棒控制方法，是對時間域或頻率域來說，一般要假設過程動態特性的信息和它的變化範圍。一些算法不需要精確的過程模型，但需要一些離線辨識。
一般魯棒控制系統的設計是以一些最差的情況為基礎，因此一般系統並不工作在最優狀態。常用的設計方法有：INA方法，同時鎮定，完整性控制器設計，魯棒控制，魯棒PID控制以及魯棒極點配置，魯棒觀測器等。
魯棒控制方法適用於穩定性和可靠性作為首要目標的套用，同時過程的動態特性已知且不確定因素的變化範圍可以預估。飛機和空間飛行器的控制是這類系統的例子。
過程控制套用中，某些控制系統也可以用魯棒控制方法設計，特別是對那些比較關鍵且（1）不確定因素變化範圍大；（2）穩定裕度小的對象。
但是，魯棒控制系統的設計要由高級專家完成。一旦設計成功，就不需太多的人工干預。另一方面，如果要升級或作重大調整，系統就要重新設計。
H∞魯棒控制理論的特點
1) 將經典頻域設計理論具有一定的魯棒性和現代控制理論狀態空間方法適於M IM O 系統的兩個優點融合在一起，系統地給出了在頻域中進行迴路成形的技術和手段。
2) 給出了魯棒控制系統的設計方法，並充分考慮了系統不確定性的影響，不僅能保證控制系統的魯棒穩定性，而且能最佳化某些性能指標。
3) 採用狀態空間方法，具有時域方法精確計算和最最佳化的優點。
4) 多種控制問題均可變換為H∞魯棒控制理論的標準問題，具有一般性，並適於實際工程套用。
主要算法和理論
小增益理論
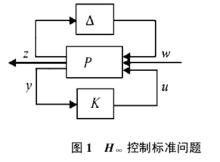
H∞範數的重要特性來自於小增益理論的套用。小增益理論如下：如果 ‖Tz w‖∞≤r, 則對所有穩定的且 ‖
‖∞< 1/r的$， 圖1 所示的系統是穩定的。其中， Tz w為從w到z 的閉環傳遞函式，P 、 K 、分別表示廣義被控對象、控制器及模型攝動，w 是外部輸入信號， 包括指令信號、干擾和感測噪聲，y 為量測輸出， u 為控制器輸出， z 為受控輸出。
迴路成形方法
圖 2給出了標準的反饋控制的系統結構。定義輸入開環傳函陣Li= K P , 輸出開環傳函陣Lo= P K，Li，Lo統稱為 L。在低頻( 0，ω) 內，好的系統性能要求
在高頻(ω1，∞) 內, 好的系統魯棒性能及好的感測器噪聲衰減要求。其中M為不太大的數。
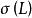穩定魯棒控制
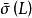穩定魯棒控制迴路成形(Loop Shaping) 概念： 迴路成形控制器設計包括找到一個控制器K，使開環傳函陣 L呈現使開環增益 和 在低頻區域滿足性能要求、在高頻區域滿足魯棒性要求的形狀，即低頻高增益、高頻低增益。
穩定魯棒控制分析方法
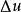穩定魯棒控制
穩定魯棒控制
穩定魯棒控制模型攝動 到底多大(以‖‖∞含義)才不會破壞反饋系統的穩定性，可用 來表示。
無靜差性
以準確地跟蹤外部參考輸入信號和完全消除擾動的影響為穩態性能指標的一類魯棒性。如果控制系統在其特性或參數的標稱值處是漸近穩定的且可實現無靜差控制（又稱輸出調節，即系統輸出對參考輸入的穩態跟蹤誤差等於零），並且對標稱值的一個鄰域內的每一種情況它也是漸近穩定和可實現無靜差控制的，那么稱此控制系統是結構無靜差的。使系統實現結構無靜差的控制器通常稱為魯棒調節器。用方程N1(D)f(t)=0 N2(D)z0(t)=0
表示加於受控系統的擾動f(t)和參考輸入z0(t)的動態模型，式中為微分運算元，N1(D)和N2(D)為D的多項式。用k1(s)和k2(s)（s為複數變數）分別表示N1(D)和N2(D)的最小多項式，而用k(s)表示k1(s)和k2(s)的最低公倍式。那么存在魯棒調節器可使受控系統T(s)z=U(s)u+M(s)f
y=z
（見多變數頻域方法）實現結構無靜差的充分必要條件是，控制向量u的維數大於輸出向量y的維數，同時對代數方程k(s)=0的所有根si(i=1，2，…,p)矩陣U(si)為滿秩。對於可實現結構無靜差的受控系統，一個動態補償器P(s)ξ=z0-z
u=R(s)ξ
（ξ為補償器的狀態向量）能構成為它的魯棒調節器的充分必要條件是，矩陣P(s)的每一個元都可被k(s)除盡，同時由受控系統和動態補償器組成的閉環控制系統是結構漸近穩定的。在採用其他形式的數學描述時，魯棒調節器和結構無靜差控制系統的這些條件的表述形式也不同。魯棒調節器在結構上有兩部分組成，一部分稱為鎮定補償器，另一部分稱為伺服補償器。鎮定補償器的功能是使控制系統實現結構漸近穩定。伺服補償器中包含有參考輸入和擾動信號的一個共同的動力學模型，因此可實現對參考輸入和擾動的無靜差控制。對於呈階躍變化的參考輸入和擾動信號，它們共同的動力學模型是一個積分器；對於呈斜坡直線變化的參考輸入信號和呈階躍變化的擾動信號，其共同的動力學模型是兩個積分器的串接。
帶有狀態觀測器的系統的魯棒性 一般而言，在控制系統中引入狀態觀測器會使它的魯棒性變壞，因此應儘可能避免。對於必須採用狀態觀測器的控制系統，當受控系統為最小相位系統時，可通過合理地設計觀測器而使控制系統保持較好的魯棒性。其原則是把觀測器的一部分極點設計成恰好與所觀測系統的零點相對消，而觀測器的其他極點在滿足抗干擾性要求的前提下應使其儘可能地遠離虛軸。
