定義
與積分相似：連續(或非連續可積)函式的連續和為積分，連續相乘即為積乘。
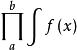積乘表示函式f(x)從a至b的積乘。其中的a,b表示f(x)中x的上下限，表示維度。而積分中的上下限表示高一維比低一維多出的那一維上的坐標。兩者性質不同 。
積乘可轉換為普通函式
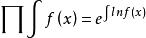積乘可積乘函式有
定義域為實數，值域為正實數的（連續）函式。
定義域為全體複數，值域為對數唯一確定的數，用
1.定義域為實數，值域為正實數的（連續）函式。
2.定義域為全體複數，值域為對數唯一確定的數，用
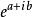積乘形式表達，對數為a+ib。
3.可對角化的矩陣，且矩陣特徵值為可積乘數。
性質
積乘表示維度上的連續變化。
於積分類似，其也可以分為不定積乘與定積乘，其也有逆運算。
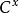積乘其為維度上的連續變化較難理解，下面以F(X)=C為例,其積乘結果為 ，定積乘結果為C的上限次方除以C的下限次方。維度為1時，結果為一維上的長度；維度為2時，結果為二維上的面積；維度為3時為三維上的體積……而積乘的連續表明維度的連續，即可以有小數次維度，甚至負數次維，複數次維等。
所以定積乘的結果一般要帶上維度的上限減下限次方作為單位，也可以省略。
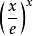積乘例1：F(X)=X.其積乘結果為
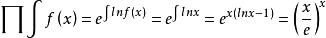積乘解：
積乘例2:
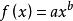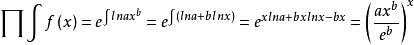積乘套用
其中一個套用就是可以推算出階乘的表達式。
n!=nx(n-1)! n>=0
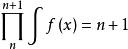積乘現在設有一函式F（X）滿足 恆成立，且該函式0至1積乘為1，則n為正整數時該函式的0至n積乘即為n的階乘。n為其他數值時取得的值可以視為階乘的拓延。
註：階乘的拓延有無數種，但我們可以選取一個較合理的視為階乘的準確拓延。現在認為萊昂哈德·歐拉 先生髮現的伽瑪函式 即為階乘的拓延。
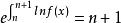積乘解：由上式可得
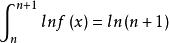積乘
連乘推階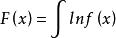乘
積乘設
則 F(n+1)-F(n)=ln(n+1)恆成立
關鍵步驟：兩邊同時求導得
F`(n+1)-F`(n)=ln`(n+1)
lnf(n+1)-lnf(n)=1/(n+1)
調和級數的拓延函式G(x)有相同的性質
G(n+1)-G(n)=1/(n+1) n>0恆成立。
則令lnf(x)=G(x)+C C為特定常量
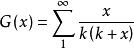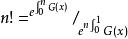積乘
積乘作為參照函式可得
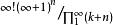積乘=
在n為常量時此時完全可用，但當n 趨於無窮時此時失準。
用
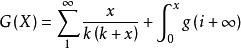積乘可以得到階乘的精準拓延公式。
微商
微商為積乘的逆運算。即微商的積乘等於原式。
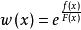積乘微商w(x)於原式F(x)有以下關係
其中f(x)為原式F(x)的導函式。
推導如下：
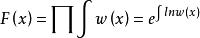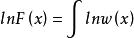積乘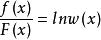
積乘
積乘兩邊同時求導得：
其中f(x)為原式F(x)的導函式
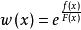積乘由此式可以推出很多函式的微商，如：
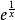積乘F(x)=x w(x)=
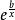積乘F(x)=ax^b w(x)=
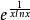積乘F(x)=lnx w(x)=
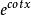積乘F(x)=sinx w(x)=
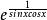積乘F(x)=tanx w(x)=
等等
用積乘方法求球連續轉動後的方向變化矩陣
在標準正交基向量下，球轉動後方向改變，相當於用一個矩陣乘以某向量在球轉動前的坐標值而得到其在球轉動後的坐標值。而兩次轉動的疊加為矩陣按前後順序相乘。一段連續轉動，我們將時間間隔不斷縮小，然後將每段時間的轉化矩陣按時間先後相乘，即可以不斷的逼近整段時間轉動的轉化矩陣。
而利用積乘方法可以直接推出個時間點的轉化矩陣。
球轉動方向轉化矩陣推導過程