定義
按照是否具有周期重複性,確知信號可以分為周期信號(periodic signal)和非周期信號(nonperiodic signal)。周期信號的典型實例有正弦信號,其表達式為f(t)=Ksin(ωt+θ),式中K是振幅,ω是角頻率,θ稱為初相位。
非周期信號的典型實例有指數信號,其表達式為f(t)=Ke,式中a為實數。若a>0,則信號將隨時間按指數律增長,若a<0,信號將隨時間按指數律衰減。在a=0的特殊情況下,信號不隨時間而變。常數K表示指數信號在t=0時的初始值。以上兩例均屬連續時間信號。
離散時間信號在時間上是離散的,只在某些不連續的規定瞬時有確定的函式值,在其它時間沒有定義。一般以x(n)表示,其中n為整數,即規定的時間瞬時。離散時間信號中也有周期信號與非周期信號之分。
確知信號的分類
 確知信號
確知信號周期信號:
其中T0即為信號的周期, T0 > 0 ,將1/To稱為基頻fo,且T0為一常數,則稱此信號為周期信號,否則為非周期信號。
非周期信號:沒有最小正周期的信號,即稱為非周期信號。單個矩形脈衝、衝激信號就是非周期信號。
能量信號:按照能量是否有限來與功率信號進行區分,若信號的能量有限,為一個有限正值,則將其稱為能量信號,即滿足下式即為能量信號。其特徵是:信號的振幅和持續時間均有限,非周期性。例如,單個矩形脈衝。
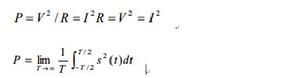 圖1
圖1功率信號:在通信理論中,通常把信號功率定義為電流在單位電阻(1 Q)上消耗的功率,即歸一化( normalized)功率Po.
式中:V為電壓(V);I為電流(A)。
能量信號的功率趨於0,功率信號的能量趨於正無窮,但功率信號的平均功率P等於一個有限正值。功率信號的持續時間無限。例如:直流信號、周期信號。
確知信號的頻域性質
確知信號在頻域(frequency domain)中的性質,即頻率特性,由其各個頻率分量的分布表示,可以用頻譜、頻譜密度、能量譜密度和功率譜密度來描述,通過運用傅立葉( Fourier)級數和傅立葉變換來實現。傅立葉級數適用於周期信號,而傅立葉變換則對周期信號和非周期信號都適用。
1 周期信號的傅立葉級數
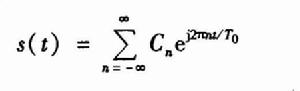 圖2
圖2設s(t)是一個周期為To的周期功率信號。若它滿足狄利克雷(Dirichlet)條件,則可展開成如圖2的指數型傅立葉級數。
其中,傅立葉級數的係數為如圖3:
式中,f0=l/T0稱為信號的基頻,基頻的n倍(n為整數,- ∞ <n<+∞)稱為幾次諧波頻率。
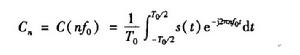 圖3
圖32 周期信號的傅立葉級數
一個非周期確知信號s(t)的傅立葉變換和反變換關係式如圖4
上述傅立葉變換積分的充分條件是:s(t)在一∞和+∞間絕對可積,以及s(t)的任意間斷點為有窮值。
 圖4
圖4總結
確知信號按照其強度可以分為能量信號和功率信號。功率信號按照其有無周期性劃分,又可以分為周期性信號和非周期性信號。能量信號的振幅和持續時間都是有限的,其能量有限,(在無限長的時間上)平均功率為零。功率信號的持續時間無限,故其能量為無窮大。確知信號的性質可以從頻域和時域兩方面研究。確知信號在頻域中的性質有四種,即頻譜、頻譜密度、能量譜密度和功率譜密度。周期性功率信號的波形可以用傅立葉級數表示,級數的各項構成信號的離散頻譜,其單位是Vo能量信號的波形可以用傅立葉變換表示,波形變換得出的函式是信號的頻譜密度,其單位是V/Hzo只要引入衝激函式,我們同樣可以對於一個功率信號求出其頻譜密度。能量譜密度是能量信號的能量在頻域中的分布,其單位是J/Hz o功率譜密度則是功率信號的功率在頻域中的分布,其單位是W/Hzo周期性信號的功率譜密度是由離散譜線組成的,這些譜線就是信號在各次諧波上的功率分量I Cn 12,稱為功率譜,其單位為Wo但是,若用6函式表示此譜線,則可以寫成功率譜密度IC(f)1 2艿(f -氓)的形式。確知信號在時域中的特性主要有自相關函式和互相關函式。自相關函式反映一個信號在不同時間上取值的關聯程度。能量信號的自相關函式R(O)等於信號的能量;而功率信號的自相關函式R(O)等於信號的平均功率。互相關函式反映兩個信號的相關程度,它和時間無關,只和時間差有關。並且,互相關函式和兩個信號相乘的前後次序有關。能量信號的自相關函式和其能量譜密度構成一對傅立葉變換。周期性功率信號的自相關函式和其功率譜密度構成一對傅立葉變換。
