定義
上界和下界
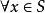 確界原理
確界原理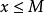 確界原理
確界原理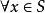 確界原理
確界原理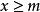 確界原理
確界原理設實數集S非空。若存在實數M, ,有 ,則稱M是S的一個上界。而若存在實數m, ,有 ,則稱m是S的一個下界。
顯然,所有大於M的數都是S的上界,所有小於m的數都是S的下界。因此一個數集的上界(或下界)不是唯一的。
上確界和下確界
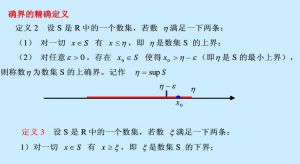
設非空數集S有上界,若存在實數β滿足以下兩個條件:
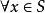 確界原理
確界原理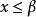 確界原理
確界原理① ,有 ;(即β是S的一個上界)
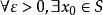 確界原理
確界原理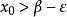 確界原理
確界原理② ,有 。(即再小一點就不是上界)
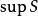 確界原理
確界原理則稱實數β為S的上確界,記為 。
同理,若存在實數α滿足以下兩個條件:
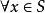 確界原理
確界原理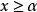 確界原理
確界原理① ,有 ;(即α是S的一個下界)
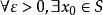 確界原理
確界原理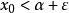 確界原理
確界原理② ,有 。(即再大一點就不是下界)
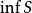 確界原理
確界原理則稱實數α為S的下確界,記為 。
有時上確界也被叫做最小上界,下確界也被叫做最大下界。
注意:S的上確界(或下確界)可能屬於S,也可能不屬於S。當上確界(或下確界)屬於S時,不難證明上確界(或下確界)就是S中的最大數(或最小數)。
描述
確界原理:任一有上界的非空實數集必有上確界(最小上界);同樣任一有下界的非空實數集必有下確界(最大下界)。
實數的這個性質是波爾查諾(Bolzano,B.)於1817年發現的。
證明
由戴德金定理證明非空有上界數集必有上確界,非空有下界數集必有下確界同理。
 確界原理
確界原理設S為一非空有上界數集,即 成立。取數集B為S所有上界的集合,A=R/B。則:
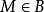 確界原理
確界原理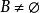 確界原理
確界原理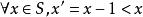 確界原理
確界原理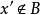 確界原理
確界原理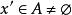 確界原理
確界原理①由取法可知 ,故 。 ,故 ,因此 。
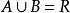 確界原理
確界原理② 。
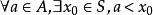 確界原理
確界原理③∵A中任何元素都不是S的上界,∴ 。
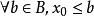 確界原理
確界原理又∵B中任何元素都是S的上界,∴ 。
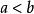 確界原理
確界原理故必有 。
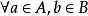 確界原理
確界原理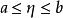 確界原理
確界原理∴由戴德金定理可知,要么A中有最大值,要么B中有最小值。設這個值為η,並且 , 恆成立。
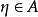 確界原理
確界原理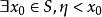 確界原理
確界原理假設η是A中的最大值,即 ,那么, 。
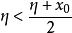 確界原理
確界原理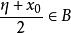 確界原理
確界原理又∵ ,∴ 。
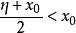 確界原理
確界原理但, ,與B中任何元素都是S的上界矛盾。
∴η是B中的最小值,即S有最小上界(上確界)。
推廣的確界原理
若把+∞和-∞補充到數集當中,並規定任意一實數a與+∞,-∞的關係為-∞<a<+∞,則確界的概念可擴充為:若數集S無上界,則規定+∞為S的非正常上確界,記做sup S=+∞;若S無下界,則定義-∞為S的非正常下確界,記做inf S=-∞,相應的,若S有上確界或者下確界,則此定義分別成為正常上確界和正常下確界。
即: 任意一非空數集必有上確界和下確界(包括正常的和非正常的)
套用
確界原理作為整個極限理論的基礎,並且由於它直觀易懂,經常代替戴德金定理作為實數公理,從而導出一系列與極限相關的性質,如單調有界定理,柯西審斂原理等。在此簡單介紹用確界原理推導柯西審斂原理。
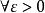 確界原理
確界原理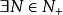 確界原理
確界原理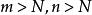 確界原理
確界原理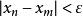 確界原理
確界原理柯西審斂原理:數列{x} 收斂的充要條件是,,,當時,有。
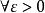 確界原理
確界原理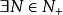 確界原理
確界原理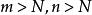 確界原理
確界原理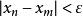 確界原理
確界原理我們把條件“,,當時,有”稱為柯西條件,把滿足柯西條件的數列稱為柯西序列,於是{x}收斂就等價於{x}是柯西序列,或{x}滿足柯西條件。
其幾何意義表示,數列{x}收斂的充要條件是,對任意給定的正數ε,在數軸上一切具有足夠大號碼的點x中,任意兩點的距離小於ε。
證明:
必要性:(略,可參考相應詞條)
充分性:先證明柯西序列是有界的。
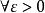 確界原理
確界原理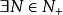 確界原理
確界原理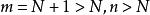 確界原理
確界原理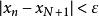 確界原理
確界原理因{x}是柯西序列,,,當時,有。
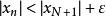 確界原理
確界原理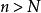 確界原理
確界原理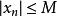 確界原理
確界原理注意一旦ε確定之後,就被當做常數,於是由上述不等式以及三角不等式解得,因此當時,{x}有界。而把數列的前N項添加進去顯然還是有界的,於是得到對任意自然數n,{x}有界。設。
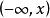 確界原理
確界原理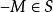 確界原理
確界原理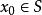 確界原理
確界原理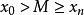 確界原理
確界原理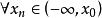 確界原理
確界原理現構造一個集合S,集合S中的元素x滿足:在區間上最多有{xn}的有限項且至少有一個{x}的項。顯然,於是S非空;而S又是有界的,M是一個上界。這是因為假設M不是上界,即存在,使得,即,與S的定義不符。
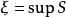 確界原理
確界原理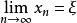 確界原理
確界原理根據確界原理,S存在上確界,設,現證。
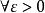 確界原理
確界原理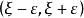 確界原理
確界原理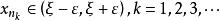 確界原理
確界原理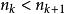 確界原理
確界原理,考慮區間,這個區間上必然有{x}的無限項。不妨設,且。
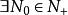 確界原理
確界原理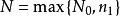 確界原理
確界原理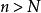 確界原理
確界原理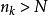 確界原理
確界原理因{x}是柯西序列,由定義,對上述的ε,,令,當時,任取某個,有
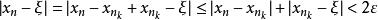 確界原理
確界原理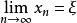 確界原理
確界原理∴