相關解調
相關的描述性定義:兩個變數相乘以後求平均。比如隨機變數的相關是E[XY],兩個信號的相關是乘積後按時間的平均(或者積分,注意時間平均和時間積分只是係數的差別,我們用有實際意義的那個,如能量信號用能量,功率信號用功率)。
相關接收機信乾噪比損耗隨著干擾頻寬和干擾強度的增加而增大,隨干擾頻率與中心頻率偏差和噪聲頻寬的增加而減小 。
相干解調
相干的描述性定義:兩個電磁波或者光,如果它們的相位有確定的聯繫,就是相干的。與此不同的是非相干,指它們的相位毫無關係,如非相干光。
相干解調錶明本地的載波和傳送載波同頻同相(如果是固定相差,很容易校正,令我們頭疼的是不確定的隨機相差,注意頻差無非是時變的相差)。非相干解調錶明不必care傳送的載波相位是多少。例如OOK檢測信號強度、FSK檢測某個頻率是否出現,這樣的檢測都不需要知道傳送載波的相位具體是多少(FSK如同我們檢測紅光和藍光那個存在,顯然這樣的檢測不要求我們必須知道這兩個光的確切相位是多少)。而檢測BPSK、DSB-SC就得知道傳送相位是多少。
相關解調器
(1)根據傳送信號集,構造正交基。
即:傳送信號可能的種類數為M,但維數只有N。
 構造相關解調器
構造相關解調器要求:中每一個信號都可以表示成的加權線性。
注意,正交基的構造不考慮噪聲空間。
疊加了信道噪聲後,接收信號理論上可以分解。
(2)得到接收信號在各基函式上的投影
令接收信號通過一組並行的個互相關器。
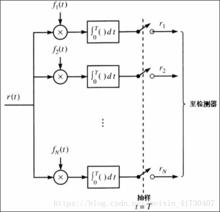 互相關器
互相關器高斯隨機變數,由信道引入的加性噪聲決定。
接收機
接收機有兩種基本構成結構,一種是超外差(superhetrodyne)結構,另一種是直接轉換結構。
所謂超外差接收機,就是將接收到的射頻信號與某一頻率的本振信號進行混頻或下變頻之後輸出一個頻率較低的中頻調製信號,該中頻信號的頻率就是本振信號和被接收的信號的頻率之間的固定頻差。最終信號的解調是將中頻信號濾波、放大後在中頻上由解調器完成,改變接收機平均次數分離,以及改變發射功率的同時,改變接收機中頻頻寬 。
在直接轉換接收機中,其基本原理同於外差接收機,不同之處在於參與混頻的本振頻率不是任意給定的,而是等於載波頻率,這樣中頻頻率就為0,所以再不存在鏡像頻率與鏡頻干擾,這種方案通常稱為零中頻方案。該方案的射頻部分省去了鏡頻濾波器,而中頻濾波器變成了低通濾波器,簡化了系統的構成,降低了設計和實現的難度,節約了成本。但是直接轉換接收機存在明顯的缺點,如由於本振的頻率和載波頻率相同,故容易造成本振的泄漏;存在直流偏差,對隨後的電路造成嚴重影響;只能用於調幅信號的解調,不能解調調頻和調相信號;對本振的穩定性要求高,所以多數只在低頻段使用。
白噪聲
就是說功率譜為一常數;也就是說,其協方差函式(零均值)在delay=0時不為0,在delay不等於0時值為零;換句話說,樣本點互不相關。所以,“白”與“不白”是和分布沒有關係的。當隨機的從高斯分布中獲取採樣值時,採樣點所組成的隨機過程就是“高斯白噪聲”,高斯白噪聲代表最大的隨機性,因而在諸多的仿真中都採用高斯白噪聲。同理,當隨機的從均勻分布中獲取採樣值時,採樣點所組成的隨機過程就是“均勻白噪聲”。
那么,是否有“非白的高斯”噪聲呢?答案是肯定的,這就是”高斯色噪聲“。這種噪聲其分布是高斯的,但是它的頻譜不是一個常數,或者說,對高斯信號採樣的時候不是隨機採樣的,而是按照某種規律來採樣的。
而“高斯”與“白”沒有直接關係有時人們還會提出高斯型噪聲,這指的是噪聲功率譜呈高斯分布函式的形狀而已。
關於最大隨機性,雖然文獻中沒有“最大隨機性”這種說法,但是這種說法也有道理。我們討論的隨機過程一般都是二階矩過程,這種隨機過程一般都只涉及其均值函式和相關函式的討論,白噪聲的相關函式只有在0處不為零,其他處處不為零,因此白噪聲過程除了在同一時刻上的值相關以外,其它時刻上的值處處不相關,從這個意義上來說,它的隨機性最大。而其它的隨機過程它的相關函式並沒有這種特性。

