直角投影定理

直角投影定理，垂直相交的兩直線，若其中一直線平行於某投影面，則兩直線在該投影面上的投影仍然反映直角關係。

定理

通常稱之為直角投影定理。

如下圖所示，AB、BC為相交成直角的兩直線，其中直線BC平行於H面（即水平線），直線AB為一般位置直線。現證明兩直線的水平投影ab和bc仍相互垂直，即bc⊥ab 。

證明：如圖5-15所示，因為BC⊥Bb，BC⊥AB ， 所以BC⊥平面AB ba;又因BC∥bc，所以bc也垂直於平面AB ba。根據立體幾何定理可知bc垂直於平面ABba上的所有直線，故bc⊥ab。

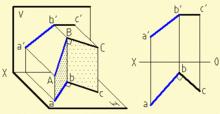圖5-15

逆定理

若相交兩直線在某一投影面上的投影為直角，且其中一條直線平行於該投影面，則該兩直線在空間必相互垂直。

[例5-5]如圖5-16所示，己知直線AB及點K的投影，過點K作直線KS與直線AB正交（交點S在直線AB上）。

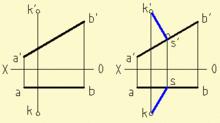圖5-16

解：根據直角投影定理，過k'作k's'⊥a'b'，交直線AB的正面投影a'b'於s',根據s'求出點S的水平投影s，連線ks，ks 及k's'即為所求。